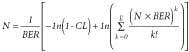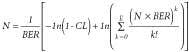Explaining those BER testing mysteries
The ultimate function of the physical layer (PHY) in any digital communications system is to transport bits of data through a medium like copper cable, optical fiber, or free space as quickly and accurately as possible. Hence, two basic measures of PHY performance relate to the speed at which the data can be transported (data rate) and the integrity of the data when they arrive at their destination. The primary measure of data integrity is called the bit-error ratio (BER).
A digital communications system's BER can be defined as the estimated probability that any bit transmitted through the system will be received in error (e.g., a transmitted "1" will be received as a "0" and vice versa). In practical tests, the BER is measured by transmitting a finite number of bits through the system and counting the number of bit errors received. The ratio of the number of bits received erroneously to the total number of bits transmitted is the BER. The quality of the BER estimation increases as the total number of transmitted bits increases. In the limit, as the number of transmitted bits approaches infinity, the BER becomes a perfect estimate of the true error probability.
In some texts, BERis referred to as the bit-error rate instead of bit-error ratio. Most bit errors in real systems are the result of random noise and therefore occur at random times as opposed to an evenly distributed rate. Also, BER is an estimate formed by taking a ratio of errors to bits transmitted. For these reasons, it is more accurate to use the word "ratio" in place of "rate."
Depending on the particular sequence of bits (i.e., data pattern) transmitted through a system, different numbers of bit errors may occur. Patterns that contain long strings of consecutive identical digits (CIDs), for example, may contain significant low-frequency spectral components that might be outside the passband of the system, causing deterministic jitter and other distortions to the signal. These pattern-dependent effects can increase or decrease the probability that a bit error will occur. That means when the BER is tested using dissimilar data patterns, it is possible to get different results. Without getting into a detailed analysis of pattern-dependent effects, it is sufficient to note the importance of associating a specific data pattern with BER specifications and test results.
Most digital communications protocols require BER performance at one of two levels. Telecommunications protocols such as SONET generally require a BER of one error in 1010 bits (i.e., BER=1/1010=10-10) using long pseudo-random bit patterns. In contrast, data communications protocols like Fibre Channel and Ethernet commonly specify a BER of better than 10-12 using shorter bit patterns. In some cases, system specifications require a BER of 10-16 or lower.
It is important to note that BER is essentially a statistical average and therefore only valid for a sufficiently large number of bits. It is possible, for example, to have more than one error within a group of 1010 bits and still meet a 10-10 BER specification when the total number of transmitted bits is much greater than 1010. That could happen if there is less than one error in 1010 bits for subsequent portions of the bit stream. Alternately, it is possible to have zero errors within a group of 1010 bits and still violate a 10-10 standard. In light of these examples, it is clear that a system that specifies a BER better than 10-10 must be tested by transmitting significantly more than 1010 bits.
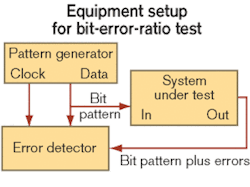
Conventional BER testing uses a pattern generator and an error detector (see Figure 1). The pattern generator transmits the test pattern into the system under test (SUT). The error detector either independently generates the same test pattern orreceives it from the pattern generator. The pattern generator also supplies a synchronizing clock signal to the error detector, which performs a bit-for-bit comparison between the data received from the SUT and the data received from the pattern generator. Any differences between the two sets of data are counted as bit errors.As noted in the previous section, digital communications standards typically specify the data pattern to be used for BER testing. A test pattern is usually chosen that emulates the type of data expected to occur during normal operation, or in some cases a pattern may be chosen that is particularly stressful to the system for "worst-case" testing. Patterns intended to emulate random data are called pseudo-random bit sequences (PRBSs) and based on standardized generation algorithms. PRBS patterns are classified by the length of the pattern and generally referred to by such names as 27-1 (pattern length = 127 bits) or 223-1 (pattern length = 8,388,607). Other patterns emulate coded/scrambled data or stressful data sequences and are given names like K28.5 (used by Fibre Channel and Ethernet). Commercially available pattern generators include standard built-in patterns as well as the capability to create custom patterns.
To accurately compare the bits received from the pattern generator to the bits received from the SUT, the error detector must be synchronized to both bit streams and compensate for the time delay through the SUT. A clock signal from the pattern generator provides synchronization for the bits received from the pattern generator. The error detector adds a variable time delay to the pattern-generator clock to allow synchronization with bits from the SUT. As part of the pre-test system calibration, the variable time delay is adjusted to minimize bit errors.
In a well-designed system, BER performance is limited by random noise and/or random jitter. The result is that bit errors occur at random (unpredictable) times that can be bunched together or spread apart. Consequently, the number of errors that will occur over the lifetime of the system is a random variable that cannot be predicted exactly. The true answer to the question of how many bits must be transmitted through the system for a perfect BER test is therefore unbounded (essentially infinite).
Since practical BER testing requires finite test times, we must accept less than perfect estimation. As previously noted, the quality of the BER estimation increases as the total number of transmitted bits increases. The problem is how to quantify the increased quality of the estimate so that we can determine how many transmitted bits are sufficient for the desired estimate quality. That can be done using the concept of statistical confidence levels (CLs). In statistical terms, the BER CL can be defined as the probability-based on E detected errors out of N transmitted bits-that the "true" BER would be less than a specifiedratio R. (For purposes of this definition, true BER means the BER that would be measured if the number of transmitted bits was infinite.) Mathematically, that can be expressed as:
CL = PROB [BERT
where CL represents the BER confidence level, PROB[ ] indicates "probability that," and BERT is the true BER. Since CL is by definition a probability, the range of possible values is 0% to 100%. Once the CL has been computed, we may say that we have CL percent confidence that the true BER is less than R. Another interpretation is that if we were to repeatedly transmit the same number of bits N through the system and count the number of detected errors E each time we repeated the test, we would expect the resulting BER estimate E/N to be less than R for CL percent of the repeated tests.
As interesting as the equation is, what we really want to know is how to turn it around so that we can calculate how many bits need to be transmitted to calculate the CL. To do that, we make use of statistical methods involving the binomial distribution function and Poisson theorem.1 The resulting equation is:where E represents the total number of errors detected and ln[ ] is the natural logarithm. When there are no errors detected (i.e., E=0), the second term in this equation is equal to zero and the solution to the equation is greatly simplified. When E is not zero, the equation can still be solved empirically (e.g., using a computer spreadsheet).
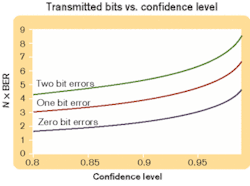
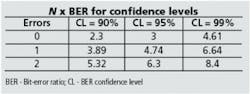
As an example of how to use the equation, let's assume that we want to determine how many bits must be transmitted error-free through a system for a 95% CL that the true BER is <10-10. In this example E=0, so the second term (the summation) is zero, and we only have to be concerned with CL and BER. The result is N = 1/BER × [-ln(1-0.95)] ≈ 3/BER = 3 = 1010. This result illustrates a simple "rule of thumb"-the transmission of three times the reciprocal of the specified BER without an error gives a 95% CL that the system meets the BER specification. Similar calculations show that N = 2.3/BER for 90% confidence or 4.6/BER for 99% confidence if no errors are detected.Figure 2 illustrates the relationship between the number of bits that must be transmitted (normalized to the BER) versus CL for zero, one, and two bit errors. Results for commonly used CLs of 90%, 95%, and 99% are tabulated in Table. To use the graph in Figure 2, select the desired CL and draw a vertical line up from that point on the horizontal axis until it intersects the curve for the number of errors detected during the test. From that intersection point, draw a horizontal line to the left until it intersects the vertical axis to determine the normalized number of bits that must be transmitted, N × BER. Divide this number by the specified BER to get the number of bits that must be transmitted for the desired CL.
Tests that require a high CL and/or low BER may take a long time, especially for low-data-rate systems. Consider a 99% CL test for a BER of 10-12 on a 622-Mbit/sec system. From the Table, the required number of bits is 4.61 × 1012 forzero errors. At 622 Mbits/sec, the test time would be 4.6 × 1012 bits/622 × 106 bits/sec = 7,411 sec, which is slightly more than two hours. That amount of time is generally too long for a practical test, but what can be done to reduce it?
One common method of shortening test time involves intentional reduction of the signal-to-noise ratio (SNR) of the system by a known quantity during testing. That results in more bit errors and a quicker measurement of the resultant degraded BER.2 If we know the relationship between SNR and BER, then the degraded BER results can be extrapolated to estimate the BER of interest. Implementation of this method is based on the assumption that thermal (Gaussian) noise at the input to the receiver is the dominant cause of bit errors in the system.
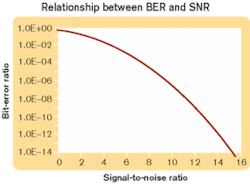
The relationship between SNR and BER can be derived using Gaussian statistics and is documented in many communications textbooks. While there is no known closed-form solution to the SNR/BER relationship, results can be obtained through numerical integration. One convenient method to compute this relationship is to use the Microsoft Excel standard normal distribution function, NORMSDIST[ ], whereby the relationship between signal-to-noise ratio and bit-error ratio can be computed as:
BER = 1- NORMSDIST(SNR/2).
Figure 3 is a graphical representation of this relationship. To illustrate this method of accelerated testing, we refer to the example in which a 99% CL test for a BER of 10-12 on a 622-Mbit/sec system would take more than two hours. From Figure 3, we see that a BER of 10-12 corresponds to an SNR of about 14. In the communications system under test, we can interrupt the signal channel between the transmitter and receiver and insert an attenuator. Since the signal is attenuated before its input to the receiver, then based on the assumption that the dominant noise source is at the receiver input, we will attenuate the signal but not the noise. Therefore, the SNR will be reduced by the same amount as the signal. Note that it is important to ensure the signal is not attenuated below the noise level of the channel.For this example, we reduce the SNR from 14 to 12 by using a 14.3% (0.67 dB) attenuation. From Figure 3, we note that reducing the SNR to 12 corresponds to changing the BER to 10-9. For a 99% BER CL at a BER of10-9, we need to transmit 4.61 × 109 bits (a factor of 1,000 less than the original test) for a test time of 7.41 sec. So if we test for 7.41 sec with no errors using the attenuator, then by extrapolation we determine that when the attenuation is removed the BER should be 10-12. Sounds great, right?
As in all things, reducing the test time through SNR reduction and extrapolation comes with a price. The price is a reduced confidence level after the extrapolation-a reduction that becomes more significant as the extrapolation distance becomes larger. To visualize this effect, consider a test in which SNR attenuation results in a reduction in BER by a factor of 100. If the SNR attenuated test is done to a 99% CL with zero errors, then we would expect that repeating the test 100 times would result in 99 tests with zero errors and one test with a single error. Now, if we concatenate all of the received bits from the 100 repeated tests, we would have 100 times as many bits with one error. Extrapolation of results from the 100 repeated tests to the original non-reduced BER level gives one error in 1/BER bits or N × BER = 1. Using the equation:we see that the corresponding CL is only 63%, low enough that it is off the chart of Figure 2 and nowhere near the 99% CL we started with.
In light of this example, the SNR should be attenuated as little as possible to achieve a practical test time. It must be realized that extrapolation will reduce the confidence level. Also, measurements and calculations must be performed with extra precision since errors introduced due to rounding, measurement tolerances, etc., will be multiplied when theresults are extrapolated.
Justin Redd is a senior strategic applications engineer in the High-Frequency/Fiber Communications Group at Maxim Integrated Products (Hillsboro, OR). He can be reached at [email protected].
- J. Redd, "Calculating Statistical Confidence Levels for Error-Probability Estimates," Lightwave, pp. 110-114, April 2000.
- D.H. Wolaver, "Measure Error Rates Quickly and Accurately," Electronic Design, pp. 89-98, May 30, 1995.