Crosstalk in cable-TV WDM systems
Mary Phillips and Dan Ott
Scientific-Atlanta
Wavelength-division multiplexing (WDM) is the technique of sending several signals on different wavelengths simultaneously through a common optical fiber. It enables information capacity to be increased without additional transmission fibers. WDM also allows segmentation of a signal to different destinations using a single fiber and no electrical processing. These capabilities are very attractive to cable-TV operators that want to send "narrowcast" signals to smaller groups of subscribers. The narrowcast signal can include premium entertainment video channels, data, and video on demand (VOD), among other services.
Ideally, the WDM signals travel down the fiber and are separated at the end with no cross-contamination. In reality, the multiplexer, fiber, and demultiplexer are not perfect and some contamination, known as crosstalk, occurs between the channels. The optical crosstalk mechanisms discussed here are present in all WDM systems. Compared to baseband digital systems, however, cable-TV lightwave systems typically transmit at a higher average optical power and over shorter distances and are more sensitive to very low levels of noise and distortion. Therefore, some sources of crosstalk that present no problem in baseband digital-transmission links can be significant in cable-TV links.
The downstream cable-TV signal consists of a radio-frequency (RF) band between 50 and 860 MHz of frequency-multiplexed digital or analog signals. Even if the RF channels carry digital signals, the signals are typically multilevel and multiphase: quadrature-amplitude modulated (QAM). For example, 64-QAM requires a theoretical 28-dB signal-to-noise ratio (SNR) and 256-QAM requires 35-dB SNR to achieve a bit-error rate of 10-9. These levels are significantly higher than the 18 dB required for a binary baseband signal. Also, to keep costs down, the fiber deployed in nearly all cable-TV distribution plants is standard singlemode, so 1,550-nm systems must work with chromatic dispersion.
Crosstalk arises from the WDM system components as well as the fiber itself. The multiplexer has critical performance parameters such as insertion loss and directivity but contributes negligible crosstalk. Transmission through the optical fiber generates WDM crosstalk because the fiber material has optical nonlinearities. Through the nonlinearities, the optical power of one channel can modulate the polarization, phase, or intensity of the other channels. Since cable-TV lightwave systems are intensity-modulated direct-detection systems, only intensity modulation at the output results in crosstalk. An optical nonlinearity that generates cross-intensity modulation, therefore, directly generates crosstalk. Optical nonlinearities that produce polarization or phase modulation must be accompanied by another mechanism to convert the nonlinearities to intensity modulation.
That is where the properties of the output components, such as the WDM demultiplexer, are important. If the output components have polarization-dependent loss (PDL), polarization modulation can be converted to intensity modulation. If these components have a wavelength-dependent transmission characteristic, phase (frequency) modulation can be converted to intensity modulation. Beyond these effects, the demultiplexer also contributes crosstalk because it does not isolate the channels perfectly.
Crosstalk mechanisms that occur solely in the transmission fiber are stimulated Raman scattering (SRS) and cross-phase modulation (XPM) acting with chromatic dispersion.1 SRS is the nonlinear coupling of two signals at different wavelengths through optical phonons. The shorter-wavelength light provides gain to longer-wavelength light, which induces crosstalk on both light signals because the "pump" is depleted and the "signal" is amplified with modulated light. XPM is the result of the nonlinear refractive index of the glass. The optical power of one channel modulates the refractive index of the fiber, which induces a phase modulation on all the other channels. With chromatic dispersion in the fiber, different frequencies travel at different group velocities, and the phase modulation is converted to intensity modulation.
Crosstalk mechanisms that depend on the output stage of the WDM system include the optical Kerr effect in fiber followed by PDL,1, 2 XPM in the fiber followed by wavelength-dependent power transmission (slope), and incomplete isolation between channels.3
The nonlinear refractive index of the fiber, is such that material parallel to the light polarization, the nonlinearity is roughly three times that perpendicular to the light polarization. If one of the WDM channels is neither parallel nor perpendicular to the other-but rather has components of both-then its two polarization components will see different magnitude nonlinearities. Because the parallel and perpendicular components will receive different magnitude nonlinear phases, the polarization at the output is changed. This case is similar to the effect used in an optical Kerr shutter, except here, the induced polarization modulation occurs incidentally and is much smaller.This equation shows the dependence of crosstalk on the system parameters. Δt is the PDL (i.e., maximum transmission is 100%; minimum is 1-Δt ), t3 represents the orientation of the partial polarizer to the polarization modulation (range -1 to 1), To is the average transmission, Poke is the effective polarization overlap for this effect (0 for parallel), n2 is the nonlinear refractive index of the fiber, P2o is the average optical power of the modulated channel at the input of the fiber, l is the wavelength, Aeff is the effective mode area, a is the loss of the fiber per km, L is the length of the fiber, and d12=1/ug1-1/ug2 is the difference in the inverse group velocities of the two channels.2
The difference in the inverse group velocities appears because with chromatic dispersion, the channels walk off from one another. The optical Kerr effect with polarization-dependent loss (OKE-PDL) crosstalk mechanism is quite different than others-depending on the relative orientation of the output polarization to the axis of the PDL, it can disappear all together. Over a long distance in standard (non-polarization preserving) fiber, the output polarization fluctuates with temperature and mechanical environment of the fiber so this crosstalk fluctuates as well.
The second crosstalk mechanism that requires both nonlinear optical interaction in the fiber and a parameter of the output stage is cross-phase modulation-transmission slope (XPM-TS). Through the nonlinear refractive index in the fiber, the modulated optical power of one WDM channel induces a nonlinear phase (and nonlinear frequency) modulation on the other channels. When followed by a component with wavelength-dependent transmission (i.e., slope), the optical frequency modulation is converted to intensity modulation, generating crosstalk. This case is similar to distortion generated by transmitting a chirped signal through an amplifier with gain slope.4 It also contrasts with standard XPM in which the phase modulation is converted to intensity modulation by chromatic dispersion in the fiber.The transmission slope is defined as the relative difference in transmission for an optical frequency shift of 1 GHz. For example, a slope of 0.1 dB/GHz is 2.3% optical modulation index (OMI) per GHz. For two WDM channels, the crosstalk from XPM-TS appearing on channel 1 is calculated as shown in the following equation:
where 1-To alphaT -alphav is the slope in OMI per GHz, and rxpm is the effective polarization overlap.1 Notice that the XPM-TS crosstalk is dependent on many of the same parameters as the OKE-PDL, because both depend on the accumulated nonlinear phase generated by the nonlinear refractive index. The predicted XPM-TS crosstalk for 7-dBm average optical power is shown in Figure 1. As a point of reference, measurements of ports of several commercial demultiplexers showed an average slope of 0.02 dB/GHz and maximum slope of 0.11 dB/GHz within their 1-dB passbands. At the half-power points, the slope magnitudes ranged from 0.16 to 0.29 dB/GHz.
Another source of crosstalk in WDM systems is well-known linear crosstalk from incomplete isolation of the channels by the demultiplexer. Unlike OKE-PDL and XPM-TS, linear cross talk does not require prior nonlinear optical interaction between the WDM channels. Linear crosstalk at the output port of channel 1 is determined using the following equation:Figure 3. Measured and calculated crosstalk at 50, 200, and 800 MHz for a fixed large transmission slope of 0.42 dB/GHz. The solid line is the total crosstalk and the dotted line is the cross-phase modulation-transmission slope crosstalk. The average power of the modulated wavelength channel is 10.1 dBm. The continuous-wave channel has average power of 6.2 dBm at 1,551.53 nm. The input polarizations are parallel and output is adjusted to maximize received power (and minimize crosstalk from optical Kerr effect with polarization-dependent loss).
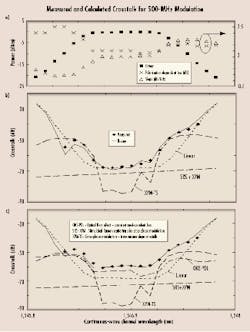
To test the theory, two 1,550-nm wavelength channels were transmitted over standard fiber as shown in Figure 2. Imperfect filtering was investigated by tuning the received channel wavelength off the passband of the demultiplexer port. Figure 3 shows results for the continuous-wave (CW) channel purposely tuned to a very high slope point (0.42 dB/GHz). From Figure 3, the full subcarrier frequency and channel spacing dependence can be determined. The dotted lines are the predicted crosstalk contribution from XPM-TS (equation 2), and the solid lines show the total crosstalk. At close spacing, the 800-MHz crosstalk is much larger than that at lower frequencies. For the same magnitude phase modulation, the corresponding magnitude of frequency modulation increases linearly with modulation frequency. At larger channel spacings, this difference diminishes because the walkoff between the channels affects higher frequency modulation more.Figure 4. Measured and calculated crosstalk for 500-MHz modulation. Modulated channel is at 1,548.5 nm, and each channel has 6.2-dBm average power at the fiber input ("A" in Figure 2). Shown here are (a) the measured transmission, transmission slope, and polarization-dependent loss; (b) the crosstalk for polarization adjusted to minimize optical Kerr effect with polarization-dependent loss (OKE-PDL) crosstalk; and (c) maximum crosstalk. In (b) and (c), the solid line is the calculated total crosstalk. The dashed lines show the calculated contributions from linear crosstalk (equation 3), stimulated Raman scattering, and cross-phase modulation (reference 2), OKE-PDL (equation 1), and cross-phase modulation-transmission slope (equation 2).
Figure 4 shows measured and predicted crosstalk at 500 MHz for wavelengths throughout a port passband. Figure 4a shows the transmission, PDL, and slope of the port. The theoretical crosstalk includes contributions from the linear, XPM-TS, OKE-PDL, SRS, and XPM mechanisms. For the polarization condition of Figure 4b, in which the launch polarizations are parallel, the OKE-PDL crosstalk is negligible. Even at the center of the passband, the linear crosstalk is larger than any other contribution. The XPM-TS crosstalk (equation 2) rises significantly at the edges of the passband. Even at some wavelengths within the 1-dB passband, it is the largest source of crosstalk. In Figure 4c, polarizations have been adjusted to maximize crosstalk. Here the OKE-PDL crosstalk is significant throughout the usable passband and increases significantly outside the passband, because the PDL increases significantly.
The linear, OKE-PDL, and XPM-TS crosstalk results show that the properties of the output demultiplexer are critical to the performance of a WDM cable-TV system. For the example shown in Figure 4, the crosstalk from each of the mechanisms involving the output filter is larger than that from fiber effects alone. For the experimental system of only two WDM channels, 6 dBm per channel, and 25 km of transmission, the crosstalk is significant for many cable-TV signals.
As an example of what might be needed in a practical system, consider eight WDM channels, each carrying 256-QAM signals between 550 and 750 MHz. In theory, without error correction, the 256-QAM signal needs a carrier-to-noise (CNR) of 35 dB to keep the error rate less than 10-9. With receiver noise and degradation due to subsequent transmission through the coaxial cable plant, assume that the lightwave system requirement is 45 dB (10-dB margin over theory). Typical demultiplexers have a minimum channel-isolation specification of -25 dB. With eight uncorrelated channels, that leads to linear crosstalk of -41 dB, which is not sufficient. The linear crosstalk from imperfect channel isolation depends only on the ratio of the powers arriving at the demultiplexer, so lowering the average optical power of the channels yields no improvement. The only way to reduce the crosstalk from this effect is to improve the channel isolation of the demultiplexer or reduce the channel count.
The other effects discussed here, XPM-TS and OKE-PDL, do depend on fiber nonlinearities, so their effect can be decreased by either improving the output stage properties (transmission flatness and PDL) or decreasing the average optical power in the fiber. The lower limit of the launched optical power is determined by the power required at the receiver to overcome receiver thermal and shot noise. For example, assume a signal of 30 channels of 256-QAM, each channel at 5.2% optical modulation depth. If the receiver has an equivalent thermal noise of 7 pa/°hz and responsivity 0.9 mA/mW, a CNR of 45 dB is achieved for average received power per WDM channel of -10 dBm or greater. With 3-dB demultiplexer insertion loss and 50-km fiber (loss 12.5 dB), the launch power per WDM channel must be 5.5 dBm. A receiver with less thermal noise or a demultiplexer with lower insertion loss could reduce this required power. If we assume a PDL of 0.2 dB, the expected crosstalk from OKE-PDL is -58 dB. Assuming a slope of 0.1 dB/GHz, the crosstalk from XPM-TS is -52 dB. While these crosstalk levels are significantly better than the requirement of -45 dB, the total crosstalk of the same system, including SRS, XPM, and linear crosstalk (assume average isolation of -30 dB), is -46 dB, which is close to the target of -45 dB.
This example shows that the specifications of the output-stage components of a WDM cable-TV system are critical for designing a successful system. Today's commercial demultiplexers typically have no specification at all for transmission slope. And a minimum channel isolation of -25 dB is not uncommon. While typical performance of demultiplexers is adequate for lower-capacity systems carrying fewer WDM channels or 16-QAM or 64-QAM signals, the successful deployment of high-capacity systems will require considerable collaboration between system designers and component manufacturers to guarantee performance.
Mary Phillips is senior electrical staff engineer and Dan Ott is senior electrical engineering associate for Scientific-Atlanta (Naperville, IL).
- M.R. Phillips and D.M. Ott, "Crosstalk due to optical fiber nonlinearities in WDM CATV lightwave systems," J. Lightwave Tech., vol. 17, pp. 1782-92, October 1999, and references therein.
- M.R. Phillips and D.M. Ott, "WDM lightwave system crosstalk by optical Kerr effect with polarization-dependent loss," Electronics Letters, vol. 35, pp. 1764-65, Sept. 20, 1999.
- M.R. Phillips and D.M. Ott, Optical Fiber Communication Conference 2000, Post-deadline paper PD6, 2000.
- C.Y. Kuo and E.E. Bergmann, "Erbium-doped fiber amplifier second-order distortion in analog links and electronic compensation," IEEE Phot. Tech. Lett., vol. 3, pp. 829-31, September 1991.