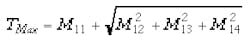An evaluation of polarization-dependent loss-characterization methods

With channel counts and speeds increasing, measuring polarization loss has become increasingly more important. But how do you do it?

John Kim and Richard Buerli
RIFOCS Corp.

The increased deployment of DWDM fiber-optic networks and the resulting discoveries regarding crucial performance parameters are driving the demand for new optical testing methods.

Polarization-dependent loss (PDL) has thus emerged as one of the essential parameters for the characteriza tion of DWDM components in fiber-optic systems.

Figure 1. Polarization comes in several forms, each represented as two vector components. Three of the more well-defined polarization states are shown here.

The distributed-feedback (DFB) lasers used as network transmitters in these systems typically produce a highly linear polarized output. However, the transmission fibers, optical amplifiers, demultiplexers, and other ancillary devices in DWDM systems do not maintain this linear polarization. It is, therefore, extremely impractical to actively control the state of polarization throughout a fiber-optic network.

Since the state of polarization is essentially unknown at various points along the network, manufacturers must screen all incorporated devices to determine the polarization sensitivity of the components used. By quantifying the variations for any possible state of polarization, a worst-case specification can be established and the corresponding loss power budget can be factored into the overall system design.

The need for polarization screening fuels the demand for reliable, efficient, and cost-effective measurement techniques to obtain PDL characterization. Several methods are currently in use to characterize PDL.

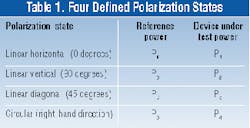
A polarized signal, according to electromagnetic theory, describes a wave in which all the transverse electric-field components are defined in a fixed-phase relationship. Unpolarized signals such as the emissions from a broadband LED source, do not have a fixed-phase relationship between electric-field components; the phase relationship may vary statistically or quasi-randomly.

Figure 2. The Poincare Sphere shows all states simultaneously. Linear polarization states are assigned to the "equator" of the sphere and circular states to the poles.

The electric fields of a lightwave signal can be represented as two vector components, Ex and Ey, which are orthogonal in an arbitrarily defined reference frame. Any state of polarization can be defined by varying the magnitude and phase relationships of these two vectors. Some well-defined polarization states, along with the corresponding Ex and Ey relationships, are shown in Figure 1.

The state of polarization (SoP) can be represented in a variety of ways. One, the Stokes Vector, describes the SoP as a 4x1 matrix. Each matrix element represents a measured power level:

S0 = Average power of entire light beam.
S1 = Power difference between horizontal and vertical linear polarization components.
S2 = Power difference between +45- and -45-degree linear diagonal polarization components.
S3 = Power difference between right-hand and left-hand circular polarization components.

Alternatively, the state of polarization can be illustrated graphically using a Poincare Sphere (see Figure 2), which is an ideal format for observing changes in polarization since all states can be viewed simultaneously. The Poincare Sphere maps each state of polarization to a particular location. Linear polarization states are assigned to the equator of the sphere, and circular states are assigned to the poles.

Figure 3. In simplest terms, polarization-dependent loss is the measurement of device output while exposing input to all possible polarization states.

PDL can be an elusive parameter to measure. In most cases, this elusiveness is not attributable to changes in the actual polarization sensitivity of the device, but is instead due to unknown, random variations in the state of polarization of the input signal. In the simplest sense, PDL can be defined as the peak-to-peak power-throughput variation measured at the output of a device, while the input is exposed to all possible states of polarization (see Figures 3 and 4).

PDL appears as a random or unrepeatable variation in the overall insertion loss of the device. Furthermore, the PDL of a component may vary depending on the input wavelength of the source. Virtually all fiber-optic components exhibit some degree of polarization sensitivity. Some typical PDL values for various components are listed in Table 1.

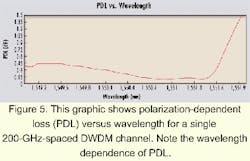
For DWDM components, polarization sensitivity is usually low for fiber gratings, while PDL values tend to be higher for thin-film-filter and other integrated optic technologies. But for devices using dielectric filter technology, the PDL may vary strongly according to the input wavelength. Such devices may be optimized for performance within certain channel passbands and exhibit much greater sensitivity at wavelengths outside this window. Figure 4 illustrates the PDL versus wavelength for a single channel of a 200-GHz-spaced DWDM demultiplexer; the wavelength dependence of PDL is clearly demonstrated.

Figure 4. The peak-to-peak power variation when the device input is exposed to all polarization states may look like this graph.

It should be noted that PDL measurements do not necessarily give any information about the state of polarization of the transmitted signal.

Furthermore, PDL values alone do not necessarily correspond to the polarization transfer function of the device under test (DUT). In essence, the polarization state at the output of a component cannot be determined by its PDL value alone.

For example, free-space optics form an excellent polarization-maintaining medium (unity polarization transfer function), and they exhibit no polarization sensitivity. However, standard singlemode fiber typically has a low PDL value for short fiber lengths, yet it is not polarization-maintaining. Due to internal birefringence in the fiber, the input state of polarization will be shifted to an unknown, random state at its output. On the other hand, polarization-maintaining fiber is specially designed to maintain a linearly polarized input launch signal even if the cable is physically moved but exhibits a peculiar polarization sensitivity. Maximum throughput is achieved by launching linearly polarized light into one axis of the fiber while minimum throughput occurs by launching into the 90-degree axis.

Detailed view of the test apparatus.

For polarization-maintaining components, this ratio between maximum and minimum transmission is commonly referred to as the "extinction ratio." From the previous examples, it becomes obvious that PDL alone only indicates the overall polarization sensitivity of a component. It is important to remember that PDL cannot be used to infer information about the state of polarization at either the input or output of a device.

Several methods have been developed to measure PDL. The first three techniques described require the use of an active polarization controller. Both fiber-loop and rotating waveplate-based polarization controllers are commercially available. The fourth method requires the use of a polarization analyzer to obtain the actual state of polarization of the signal.

The first technique, the All-States method, uses a polarization controller to generate all possible states of polarization while observing the output power of the DUT. While this method is quite thorough, it is also inefficient and time-consuming. Using a programmable polarization controller and a remote PC acquisition system, a complete analysis would require approximately 9 hours. However, in theory, this method has the potential for the greatest accuracy, since the user is assured that the device is exposed to every possible polarization state.

An alternative method to reduce the required measurement time is to randomize the input polarization while monitoring the output power. By obtaining a sufficient number of samples, the PDL can be determined within an amount of statistical certainty. Increasing the number of samples allows more random polarization states to be covered, thus increasing the likelihood of observing the conditions where maximum and minimum power occur.

Figure 5. This graphic shows polarization-dependent loss (PDL) versus wavelength for a single 200-GHz-spaced DWDM channel. Note the wavelength dependence of PDL.

The scan rate of the polarization controller should not be too slow in order to minimize the overall measurement time. Similarly, to obtain the PDL at each state of polarization, that state should remain constant long enough for the receiver to obtain the optical power level. Thus, the optical power meter used should be capable of performing measurements quickly.

Figure 6. In an experiment to illustrate the Mueller-Stokes polarization-dependent loss (PDL) measurement method, technicians used the setup schematically illustrated here.

For commercially available instruments, a typical scan time of 30 sec corresponds to a PDL error of less than 2%.1 The randomization technique drastically reduces the required measurement time in comparison to the All-States method.

But to accurately measure PDL values, a scan time greater than 30 sec is still required. Furthermore, since the method is based on the randomization representing a number of points on the Poincare Sphere, the polarization generation algorithm must seed suitably random vectors. That precludes the use of manually adjusted polarization controllers, because technicians and other personnel are unlikely to produce enough varied states for the measurements to be valid.

Figure 7. As this comparison of Mueller-Stokes polarization-dependent loss (PDL) test results using taped and untaped fibers shows, fiber movements can significantly affect test results. The test performance using untaped patch cords would prove unacceptable in most environments.

A third measurement technique, known as Mueller-Stokes analysis, involves the application of well-defined polarization states to the DUT.2 Specifically, the DUT is exposed to linear horizontal, linear vertical, linear diagonal, and right-hand circular states. The optical power is measured at each polarization state, and the PDL is computed through a solution of the first-row of the DUT Mueller Transmission Matrix (see sidebar, "Mueller-Stokes calculations").

The significant advantage of this approach lies in its simplicity and ease of automation. Using a programmable polarization controller and an optical power meter, the PDL of a device may be efficiently characterized through a remote acquisition system. Thus, this method is ideal for use in automated testing systems such as those often found in component manufacturing and qualification environments. Furthermore, since only four polarization states are required, the measurement time can be quite short. At the time of this writing, the Mueller-Stokes method was proposed for adoption by Rex Craig (NIST), TIA Working group 6.1-Fiberoptic Test, Measurement and Inspection, as a working standard.3

All these methods rely on a polarization controller to generate either random or defined polarization states. An alternate method to obtain PDL values, known as the Jones Matrix, requires the use of a polarization analyzer. By measuring the state of polarization at the input and output of a component, the analyzer can obtain the Jones Matrix of the device. This complex 2x2 matrix represents the polarization transfer function of the component. Once known, a solution of the matrix will give the PDL of the component.4 The Jones Matrix is very efficient when used to characterize the PDL of a component. Since a large number of measurements is not required, the entire process can be completed in a few seconds.

Furthermore, unlike the techniques previously discussed, the Jones Matrix can give information regarding the actual polarization states present at the input and output of a component. However, the chief disadvantage of the Jones Matrix is economic. While the other methods can be simply and inexpensively implemented using a polarization state controller and a common optical power meter, a polarization analyzer is a comparatively complex and expensive instrument. Thus, for many users, the use of a polarization analyzer in conjunction with the Jones Matrix is not a cost-effective solution.

To verify the accuracy and repeatability of the Mueller-Stokes technique, the following experimental test system was assembled. A schematic of the setup is illustrated in Figure 6.

Except where noted, all measurements were performed at a nominal wavelength of 1,550 nm. The polarization controller consists of a linear polarizer, a half-wave plate, and a quarter-wave plate. The combination of the linear polarizer and wave retarders allows the user to program any arbitrary polarization state.

To achieve variable polarization sensitivity, a special test specimen was assembled. The DUT consisted of a glass plate with an antireflection coating on both sides, which was mounted on a rotator placed between two fiber-optic collimators. Fresnel's equations describe the difference in transmittance (and reflectance) of a polarized incident beam on a boundary of two dissimilar media.5

By varying the rotator and the angle of incidence, the PDL of the device can be correspondingly adjusted. A similar experiment was performed by Nyman and presented at the 1994 Optical Fiber Communication Conference.6 The photo on page 158 depicts the test apparatus and the specimen used.

The test apparatus was controlled by a remote PC, and a software application was used to perform the required Mueller-Stokes calculations. At each incident angle, several hundred measurements were performed and logged to illustrate the measurement repeatability. The measurement was duplicated using the All-States method for verification. The results are shown in Table 2.

As predicted, the PDL increases with greater incident angles. The Mueller-Stokes method exhibits good repeatability (<0.015 dB) and demonstrates reasonable correlation with the All-States method. An overall system repeatability of ±0.01 dB and absolute accuracy of ±0.05 dB can be easily achieved.

Several fiber-optic components were also characterized to indicate their nominal PDL values (see Table 3). The values for the demultiplexer are particularly interesting, since the PDL value varies at different source wavelengths.

As the data illustrates, Mueller-Stokes analysis provides an accurate and timely method for characterizing the PDL of a component. But to ensure optimal performance, several implementation issues are extremely important:

High-performance connectors should be used at all temporary joints such as the ends of the launch and receive cables. Since the Mueller-Stokes method is based on power transmission measurements, the overall system repeatability cannot exceed that of any individual connector. Ideally, all temporary joints should be made with fusion splices; however, this may not be feasible in high-volume manufacturing environments. In such situations, the use of precision fiber-optic connectors and "gold-standard" reference cables will provide adequate performance. Furthermore, proper connector care is essential for accurate measurements. In the experiment performed for this article, Diamond FC connectors were used at all junctions. Connectors were cleaned with alcohol and inspected at the beginning of each measurement cycle.
The photodetectors used in the optical power meter should have a nominally low PDL value. Detectors with high PDL will cause incorrect power measurements when the four polarization states are generated. Angled detectors, which are offset to reduce backreflections, typically suffer from greater polarization sensitivity. Alternatively, a depolarizing filter may be inserted inline with the photodetector to reduce its polarization sensitivity.
A highly stable laser source is required for accurate PDL measurements. Any short-term source power drift will directly distort the measured PDL value. This effect can be ameliorated by splitting the laser output using a 1x2 coupler before the DUT and by measuring one output branch directly. By measuring power ratios at each required Mueller-Stokes polarization state instead of optical powers, any source drift will be compensated.
Mechanical fiber stability is perhaps the most significant contributor to PDL measurement accuracy. Unfortunately, such stability can also be difficult to maintain. While such concerns are important, their effect can be minimized using straightforward measures. As mentioned previously, standard singlemode fiber is not usually polarization-maintaining. However, polarization is generally stable in singlemode fiber, provided the cable is not moved. Physical stress caused by movement will change the birefringence of the cable and shift the polarization randomly. This effect can be easily observed by twisting a singlemode fiber connected to a polarization analyzer. Several minutes are required for the singlemode fiber to relax from these stresses and the polarization state to re-stabilize. To obtain acceptable PDL measurements, all connecting fibers in the instrument chain must remain physically stable throughout the course of the entire measurement. Furthermore, the fiber used to launch light into the DUT must remain in the same physical position as it was when the initial four-state reference was performed. Since the Mueller-Stokes method relies on measurements at four well-defined polarization states, the launch cable must remain stable to preserve the same relative positions of the states during referencing and testing.

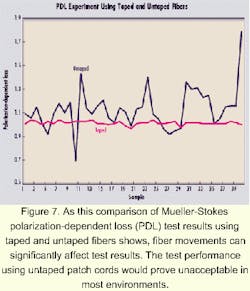
To demonstrate the effect of fiber movement on measurement performance, the PDL experiment was repeated at a few incident angles. But for this second experiment, the patch cords were not fixed using tape and instead were allowed to flex and relax over time. The results of the experiment using taped and untaped patch cords are shown in Figure 7.

The results of the second experiment illustrate that the performance using the untaped patch cords would be unacceptable in most test environments. The comparison between the data generated using fixed and loose patch cords proves the importance of keeping the connecting fibers stable.

A variety of methods currently exists for characterizing PDL. The Mueller-Stokes method is particularly attractive because of its accuracy, fast measurement time, and relatively simple implementation. Experimental data acquired using Mueller-Stokes analysis correlates well with results predicted according to theory, as well as with figures obtained using other methods. However, careful consideration of the interconnections, along with proper handling of components used during testing is crucial for ensuring acceptable accuracy and repeatability. While these conditions can usually be met in a well-controlled laboratory setting, they are much more difficult to achieve in a high-volume production environment. For designers of automated test systems, the challenge is not only to understand and implement the appropriate PDL measurement methodology, but also to provide an intelligent and efficient system of interconnections to achieve optimum measurement performance.

Richard Buerli is vice president, business units leader (Instruments Div.), and John Kim is an applications software developer at RIFOCS Corp. They can be reached at [email protected] and [email protected].

Polarization-Dependent Loss Measurements Using Modular Test System Configurations," Hewlett-Packard Product Note 11896-2, Hewlett-Packard Co. Test and Measurement Organization, Santa Clara, CA (1996).
S. Schmidt and C. Hentschel, "PDL Measurements Using the HP 8169A Polarization Controller," Hewlett-Packard Product Note, Hewlett-Packard Biblingen Instruments Div., Biblingen, Germany (1996).
R. Craig, "Measurement of Polarization Sensitivity of Single Mode Fiberoptic Components by Matrix Calculation Method," FOTP-198, TIA/EIA-455-198.
R.C. Jones, "A New Calculus for the Treatment of Optical Systems. VI. Experimental Determination of the Matrix," Journal of the Optical Society of America Vol. 37, 1947, pp. 110-112.
B.E.A. Saleh and M.C. Teich, "Fundamentals of Photonics," Wiley Series in Pure and Applied Optics, 1991, pp. 203-209.
B. Nyman, "Automated System for Measuring Polarization Dependent Loss," Optical Fiber Conference 1994 Technical Digest, 1994, pp. 230-231.

Mueller-Stokes analysis requires that four defined polarization states be synthesized. Power transmission must be measured at each state of polarization. Note that all calculations shown are for linear power units.

The reference power is obtained by first measuring the power transmission using only the launch and receive cables, without the device under test (DUT). Once the reference cycle is completed, the measurement is repeated with the DUT inserted between the launch and receive cables.The relative transmission can now be calculated along with the first row Mueller Matrix components in Table 2. Finally, the minimum and maximum transmissions along with the polarization-dependent loss (PDL) can be determined: