Handling special effects: nonlinearity, chromatic dispersion, soliton waves
As channel counts increase in carriers' networks, better knowledge of how to exploit and control fiber's phenomena is critical.
André Girard
EXFO
Nonlinear effects, chromatic dispersion, and soliton waves have been studied in physics for some time. Although not a major concern with conventional optics, the importance of understanding and controlling nonlinearity and chromatic dispersion becomes obvious when the detrimental effects these phenomena have on fiber-optic transmission are considered.
As in any other physical system, in fiber optics, nonlinearity generates spurious frequencies. In optical-communications systems, these added signals cause unexpected loss and interference in the network. Similarly, chromatic dispersion, which is caused by the dependence of the refractive index on the wavelength, induces pulse broadening, which can severely limit system transmission rates.
Although nonlinear effects and chromatic dispersion are both individually detrimental to fiber networks, the combined effects can be positive. These phenomena can interact to form waves known as optical solitons. Solitons maintain their shape over long lengths of optical fiber, especially when the pulses transmitting information have a particular form, such as Gaussian, at the input of the fiber. This phenomenon has led to the implementation of soliton-based communications systems.
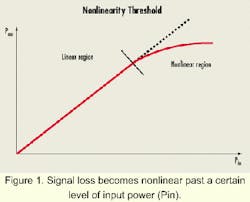
Nonlinearity in fiber is not a design or manufacturing defect; it is an inherent characteristic of electromagnetic energy passing through any medium. It occurs at high optical-intensity levels (the power per unit area) over long fiber spans. Nonlinearity is of particular concern for the designers and users of fiber-based communications systems since long-haul transmission systems rely on highly coherent laser energy to generate and transmit signals over long lengths of fiber.Nonlinear effects, which depend on the fiber's characteristics as well as the operating conditions, generally become evident after the signals have passed through a length of fiber.
These effects are noticeable when the laser signal intensity reaches a threshold value (see Figure 1). The electric field (E) of the propagating signal is proportional to the signal power (P) times the fiber nonlinear index (n2) divided by the fiber core effective area (Aeff),as expressed in the following equation:where a is the fiber attenuation co efficient, B is the phase coefficient of the propagating wave, and Y is the nonlinear coefficient equal to (2n/lamda(n2/Aeff). This nonlinear coefficient y is a key factor in nonlinear effects.
Effective area is the area of a fiber over which an assumed constant intensity will produce the same nonlinear effects as the actual varying intensity. Effective area (Aeff) is an important parameter here, because nonlinear effects increase with laser signal intensity (the power per unit area). A small effective area means higher laser-signal intensity, which leads to stronger nonlinear effects. In practice, Aeff is proportional to the core area. Generally, a fiber with a small core area will have a small Aeff; a fiber with a larger core area will have a larger Aeff.
If we assume that the light beam propagates in a Gaussian form, then Aeff = n(MFD)2/4, where MFD is the mode-field diameter. For G.6531 dispersion-shifted fibers and G.655 nonzero dispersion-shifted fibers, Aeff is equivalent to about 50 to 60 microns2, while G.652 dispersion-unshifted fibers have Aeff approximately equal to 80 microns2.Moreover, nonlinear effects increase with the length of the fiber span. Just as the core area is normalized with respect to nonlinear effects using the Aeff, the fiber span is normalized with respect to nonlinear effects using what is known as the effective fiber length (Leff). In a way analogous to Aeff, Leff is the length of fiber over which an assumed constant intensity will produce the same nonlinear effects as the actual varying intensity. For singlemode fibers, Leff is typically equal to 20 km. So in principle, for any span longer than 20 km, nonlinear effects start to accumulate in a spurious manner.
Nonlinear effects are divided into scattering phenomena and refractive-index phenomena, depending on the behavior of the nonlinear coefficient (y) in the wave propagation equation. When y is a real number, it gives rise to gain or loss caused by scattering phenomena. When y is an imaginary number, it gives rise to phase modulation caused by refractive-index phenomena.
Generally speaking, stimulated scattering arises when an incident signal is scattered, either forward or backward, through one of several possible mechanisms. In all cases, the scattered light is shifted to longer wavelengths. The magnitude of the shift and the optical spectrum of the shifted light depend on the scattering mechanism involved. Scattering phenomena are referred to as stimulated inelastic scattering, inelastic in the sense that part of the optical field's energy is transferred to the nonlinear medium.These scattering phenomena can manifest in two ways. In some instances, an acoustic phonon phenomenon called stimulated Brillouin scattering (SBS) will occur. In other cases, an optical phonon phenomenon, commonly known as stimulated Raman scattering (SRS), takes place.
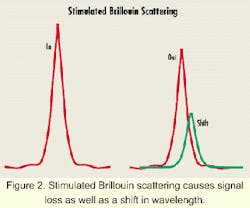
Stimulated Brillouin scattering involves sound waves, called acoustic phonons, which scatter light primarily back to the source. Incident light creates periodic regions of high refractive index-a periodic grating-that travels as a sound wave away from the light source. This "virtual grating" reflects the incident light, which is amplified as it is backscattered. Because the grating is moving forward, the reflected light is Doppler-shifted to a lower frequency or longer wavelengths.
For G.653 and G.652 fibers in the 1,550-nm window, the backscattered signal is downshifted by about 11 GHz (~0.09 nm) with a bandwidth of about 60 MHz for G.653 and 30 MHz for G.652. The Brillouin coefficient is on the order of 4x10-9 cm/W.
The importance of understanding stimulated Brillouin scattering and its causes is clear, given the adverse effects it has on fiber-optic-transmission systems. In particular, stimulated Brillouin scattering depletes signal power. It produces a ghost signal about 11 GHz from the main signal. In multiple-wavelength systems, stimulated Brillouin scattering results in short-wavelength channels amplifying long-wavelength channels, while depleting themselves especially if the channel spacign comes down to a very low valve such as 12.5 GHz or lower (see Figure 2).
Stimulated Raman scattering results from molecular vibrations caused by high power intensity. These vibrations, called optical phonons, scatter light primarily in the forward direction. The scattered light is emitted at a lower frequency (longer wavelength) than the incident light. Typically, the shift is at about 100 nm from the main signal with about 40- to 50-nm bandwidth.The effects of stimulated Raman scattering on fiber-optic-transmission systems are similar to those of stimulated Brillouin scattering. Shorter wavelength division-multiplexing (WDM) channels amplify longer wavelength channels, while their signal power is depleted. But with stimulated Raman scattering, light is downshifted to much lower frequencies compared to stimulated Brillouin. As the Raman gain coefficient is much less (~10-12) than the Brillouin, it requires a much higher power to generate effects of the same order of magnitude.
In many instances, the refractive index of a material can safely be assumed to be constant. In reality, it is not constant at all, but depends upon the intensity of the signal traveling through the medium; therefore, high optical power can cause the fiber's refractive index to change.
At low levels of signal power, fluctuations in refractive index are negligible. Past a certain power threshold, these fluctuations become more important, however. This variation in refractive index at high signal power is at the root of the nonlinear effects classified as refractive-index phenomena: self-phase modulation (SPM), cross-phase modulation (XPM), and four-wave mixing (FWM). Unlike scattering phenomena, refractive-index linear effects are elastic; as such no energy is transferred to the medium.
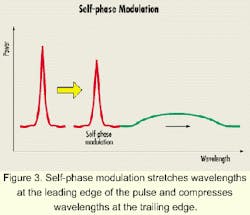
The effect that an optical pulse has on its own phase as a result of the intensity dependence of the refractive index is called self-phase modulation. The intensity peak at the center of the pulse increases the index of refraction. The higher index of refraction causes wavelengths at the center of the pulse to accumulate phase more quickly than at the wings. That stretches wavelengths at the leading edge of the pulse and compresses wavelengths at the trailing edge. Intensity variation of the pulse modulates the index, which results in modulation of the pulse's phase. This phase modulation broadens the signal spectrum (see Figure 3).
SPM aggravates pulse temporal broadening in fibers with negative chromatic dispersion and causes signal compression in fibers with positive dispersion. That is the principle behind dispersion-compensation fiber. The effect is also used with dispersion management along the fiber span and return-to-zero (RZ) modulation code to transmit signals over very long distances such as those using soliton transmissions.
In multiple-wavelength systems, SPM-induced spectral broadening of a signal can cause it to interfere with adjacent signals.
The following system characteristics can increase SPM:
- An increase in injected channel power in a fixed fiber with fixed effective area.
- An increase in the number of spans.
- An increase in the channel bit rate (higher bit rates have faster rise-and-fall bit slopes).
- Negative chromatic dispersion.
In WDM systems, SPM is more of an issue for G.652 fibers (zero dispersion at 1,310 nm) than for G.653 dispersion-shifted fibers at 1,550 nm and G.655 nonzero dispersion-shifted fibers. It is not significantly influenced by a decrease in channel spacing or by an increase in the number of channels. SPM does, however, decrease in systems with the following characteristics:
- A zero or small positive value of chromatic dispersion.
- An increase in fiber effective area.
- Dispersion compensation.
In fibers prone to loss, compensation is inexact and XPM produces spectral broadening. Chromatic dispersion converts this spectral broadening/compression to temporal broadening/compression. Negative dispersion results in spectral broadening, while positive dispersion causes spectral compression, as in the case of SPM. The XPM phenomena are less important in WDM systems using fibers with large effective areas.
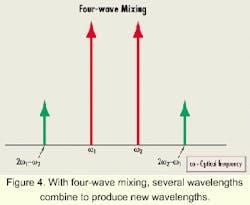
Four-wave mixing or FWM-also called four-photon mixing-is one of the most disruptive nonlinear effects in WDM systems. When the intensity of the laser signal reaches a critical level, ghost channels appear, some of which may fall within the true channels.
Past this critical signal level, an intensity modulation occurs at the beat frequency w1w2. That modulates the phase of each signal (w1 and w2) at the beat frequency, which creates two sideband frequencies (2w1-w2 and 2w2-w1). The net result of FWM is that several wavelengths mix to produce new wavelengths (see Figure 4).
The number of new wavelengths (or ghosts) is calculated as N2(N-1)/2, where N is the number of original wavelengths. Thus, 24 ghost channels appear in a 4-channel system, 224 in an 8-channel system, and 1,920 in a 16-channel system. Interference of this magnitude can be catastrophic at the receiver end.
FWM is a particularly serious issue in systems using G.653 dispersion-shifted fibers. It is less important with G.655 nonzero dispersion-shifted fibers, especially those with large effective areas. It is also not as important for dispersion-unshifted (G.652) fibers in DWDM systems at 1,550 nm, because the dispersion is relatively flat compared to dispersion-shifted (G.653) fiber, where the dispersion slope is steeper.
FWM is not significantly influenced by an increase in the channel bit rate, but it is sensitive to the following system characteristics:
- An increase in channel power or the number of spans.
- A decrease in channel spacing.
- An increase in the number of channels (although a saturation value may be reached).
FWM decreases with an increase in the fiber effective area or an increase in the absolute value of the fiber's chromatic dispersion.
All glass, including that used to make fiber, is dispersive, that is, its index of refraction varies with wavelength. Since the velocity of light in any medium depends on the refractive index, dispersion means that wavelengths propagate through fiber at different velocities.That would not present a problem if an optical channel was truly represented by a single wavelength, but even the narrowest of channels have some finite bandwidth. Sources are not completely monochromatic and a variety of intruding real-life "chirp" phenomena lead to even broader source bandwidths. Furthermore, the very act of applying modulation adds sidebands to the optical signal.
Thus, a given channel is represented by a range of closely spaced wavelengths rather than by a single wavelength. Because different wavelengths travel at different speeds (or at different group velocities), a pulse that is a sharp square at the input end of a communications link will become increasingly wide as it passes through a fiber link.
In many cases, this pulse will eventually blend into adjacent pulses, making accurate signal recovery difficult or impossible. As bit rates and link lengths increase, the effects of chromatic dispersion become greater.
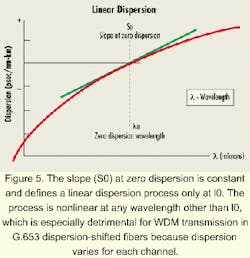
Dispersion in optical materials is complex. Although the refractive indices of most common optical materials decrease with increasing wavelength through the visible spectrum, a plot from X-ray to infrared frequencies reveals an up-and-down behavior. That means there are several regions where the behavior is just the opposite. For any given material, there are such spectral regions in which dispersion is anomalous, or contrary to expectations. Between each anomalous region and its neighboring "normal" regions lies an inflection point where the sign of the dispersion changes. Around that point is a region of zero dispersion, in which the change in refractive index with wavelength is very small. Thus, careful material selection (or preparation) can provide zero-dispersion material for fiber at and near a particular wavelength called the zero-dispersion wavelength l0.
Standard glass fiber with zero dispersion at the 1,310-nm wavelength was used for early single-wavelength systems. In the mid-1980s, dispersion-shifted fiber was produced in which the zero-dispersion point shifted to 1,550 nm (hence, the original 1,310-nm version is referred to as dispersion-unshifted).
Together with l0, designers use the S0 parameter to describe the slope of the dispersion at l0. This instantaneous slope is constant and defines a linear dispersion process only at l0. The process is nonlinear at any wavelength other than l0 (see Figure 5). That is especially detrimental for WDM transmission in G.653 dispersion-shifted fibers where dispersion varies for each WDM channel. For WDM transmissions in the 1,550-nm window, G.652 fiber has higher dispersion (about 17 psec/nm-km), but this dispersion is relatively flattened.
In the early '90s, the G.655 fiber was introduced with a varying dispersion (from about 0.1 to 10 psec/nm-km) in absolute value and a small slope (around 0.06 to 0.08 psec/nm2-km) to minimize nonlinear effects such as FWM and improve long-haul WDM transmissions (see Figure 6).
Although the variation of refractive index, and thus the group-delay variation, is a complex function of wavelength over a wide spectral range, within the very narrow band used by WDM systems, it can be considered to be linear. Thus, the chromatic dispersion for a fiber link is stated as the change in group delay per unit wavelength, in psec/nm. The delay coefficient is the dispersion for a particular fiber type and is generally quoted in units of psec/(nm-km).
Chromatic dispersion is sensitive to an increase in the number of spans, bit rate, or channel power if it results in longer span length. It is not significantly influenced by a decrease in channel spacing or by an increase in the number of channels. Its effects decrease when the absolute value of the fiber's chromatic dispersion is lowered or with dispersion compensation.
Chromatic dispersion requires more attention in WDM systems using G.652 fibers, because the dispersion is large in the 1,550-nm region, and in G.653, since the dispersion must be compensated for in each channel other than in those using G.655 fibers.
Solitons are a special type of wave, which, through the interplay of chromatic dispersion and nonlinear effects, remain undistorted over long lengths of fiber. These waves also remain intact after collision with each other. These characteristics make solitons interesting for fiber-optic-communications networks.
Optical solitons offer a solution to the simplified propagation equation. These solutions do not change with distance (z) or following a periodic pattern. More specifically, solitons result from the interplay between the group velocity dispersion (GVD) and SPM.
There are various ways of using solitons in optical-communications systems, all of which have the common goal of increasing the span of fiber between amplifiers. Solitons can be used to increase the repeater spacing at low power levels in the absence of nonlinear effects. With the advent of long-haul WDM networks, however, this application is not sufficient to make solitons useful.
Other setups are designed to provide data transmission over fiber spans approximately 1,000 km long without the need for electronic repeaters. That involves the use of optical amplifiers or Raman gain.
Several factors come into play when considering the use of solitons in fiber communications systems. Frequency chirp is a potential problem, since it can superimpose on the SPM-induced chirp. That would disturb the delicate balance between the GVD and SPM effects upon which solitons depend.
In addition, the nonlinear effects that make solitons possible can also cause disruptive interaction between neighboring solitons. That is an important consideration, because the bit-rate of a soliton-based communications network depends on how close two solitons can come without interacting with each other. By adjusting the relative phase and amplitude, the interactions between solitons can be controlled to a certain extent.
The future of fiber-optic telecommunications systems greatly depends on the methods used to control nonlinear effects and chromatic dispersion. DWDM systems, which are particularly sensitive to nonlinear effects, have already become a standard and essential technology in the industry.
For this reason, nonlinear effects, chromatic dispersion, and solitons are likely to become hot topics in the near future.
André Girard is a senior member of the technical staff at EXFO (Quebec City, Canada). Simon Evans, technical writer at EXFO, also contributed to this article.
- G.652, G.653, and G.655 refer to codes and specification documents from the International Telecommunications Union (ITU) Telecommunication Standardization Sector (ITU-T) Study Group 15, Working Party 4, Question 15 on Optical Fibers and Cables.