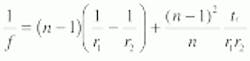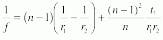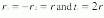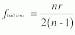Ball lenses for coupling and collimation

Ball lenses for coupling and collimation

A semiconductor technology develops a high-performance antireflection coating for ball lenses.

Donald Z. Rogers

Deposition Sciences Inc.

Ball lenses are an inexpensive, mechanically compact optical method for collimating the output of an optical fiber or laser diode. They can also be used for fiber-to-fiber, diode-to-fiber, and fiber-to-detector coupling, when access to the beam is required. Despite their inherent advantages, widespread employment of ball lenses has been limited by the difficulty in depositing high-performance, antireflection (AR) coatings on them.

Ball lens basics

A ball lens is a sphere. Ball lenses used for laser diode and fiber coupling and collimating range from 0.5 to 5 mm in diameter. Materials used include conventional optical glasses such as BK 7 and LaSF N9 as well as more exotic materials such as stabilized cubic zirconia, spinel, and sapphire. Ball lenses can be used singly to collimate the output of an optical fiber or a laser diode, or in pairs for fiber-to-fiber, fiber-to-diode, and fiber-to-detector coupling (see Fig. 1).

Figure 2 shows the most important physical and optical parameters of a ball lens. The effective focal length is the quantity used in most lens calculations, such as the one used to determine lens magnification. The general formula for the effective focal length of a lens is given by:

where: f is the effective focal length

r1 is the radius of curvature of surface 1,

r2 is the radius of curvature of surface 2,

tc is the center thickness, and

n is the index of refraction (which is a function of wavelength for a given material).

However, in the case of a sphere:

leading to the following simplified formula for the effective focal length of a ball lens:

The effective focal length is the value used in most optical calculations, and in a ball lens it is measured from the center of the lens. A more mechanically useful quantity is often the back focal length, fb, which is the distance from the lens surface to the point of focus along the optical axis. When a ball lens is used to collimate the divergent output from a laser diode or the end of an optical fiber, fb should be the distance from the end of the fiber to the edge of the ball lens.

In the case of the ball lens, the back focal length is simply:

This formula leads immediately to a very interesting result. When the index of refraction, n, of a ball lens has a value of exactly 2, then fb=0. Thus, under these conditions the point of focus occurs directly at the edge of the lens, meaning that positioning a fiber end for collimation simply involves "butt-coupling" the fiber directly to the ball lens. This condition can be met by using LaSF N35 as a lens material, as it has a refractive index of 2.02 to 1.98 in the 1310- to 1550-nm band.

Practical considerations

The primary competitor to ball lenses are gradient index (GRIN) lenses. Ball lenses have the advantages of being physically smaller and less costly than GRIN lenses, as well as significantly simpler to mount, position, and align due to their complete rotational symmetry. Also, the focal length of ball lenses is less sensitive to temperature than is the case with GRIN lenses. A shift in focal length usually results in reduced coupling efficiency, which limits the utility of GRIN lenses in field applications where they might experience wide ambient temperature swings.

On the other hand, GRIN lenses generally demonstrate superior optical performance to ball lenses. Successfully using ball lenses therefore requires an understanding of the conditions under which they can deliver the required optical performance.

The main factor that limits the optical performance of ball lenses is spherical aberration--the farther a light ray enters the lens from the optical axis, the farther it crosses the optical axis from the nominal focal point. This effect results in poor collimation, or in the case of focusing, a larger spot size. The lens parameters that determine spherical aberration are focal length, material index of refraction, and numerical aperture of operation. Numerical aperture (NA) is defined as the sine of the angle that the edge-most ray makes with the optical axis (see Fig. 2).

Spot size is determined by an interplay of these parameters. The calculation of an exact value must be performed through computer ray-tracing, which also incorporates the characteristics of the input source. But it is possible to make some generalizations that can aid in the first-order selection of the right ball lens for a specific application.

For example, spherical aberration scales with focal length (which is directly dependent upon lens diameter), so smaller-diameter ball lenses typically perform better. The tradeoff here is that smaller ball lenses require tighter positioning tolerances and can be more difficult to handle. The higher the index of refraction of a lens, the less curvature is required to achieve a given focal length. In the same way, a higher index of refraction decreases the focal length of a ball lens of a given radius. Both of these characteristics result in reduced spherical aberration, so higher-index materials perform better.

The single most important factor in determining lens performance is numerical aperture, because spherical aberration is proportional to (NA)3. Generally, this limits ball lenses to use with fibers with numerical apertures of 0.2 or less. Under these conditions, an insertion loss of about 0.4 dB can usually be achieved for fiber-to-fiber coupling using a matched pair of ball lenses.

Antireflection coatings

When light encounters an interface between two materials of differing refractive index (e.g., glass and air), part of the incident energy is reflected and part is transmitted. The exact amount reflected depends upon the index difference, the angle of incidence, and the polarization state of the light. At normal (0) incidence, material with an index of 1.5 (the approximate index of Schott BK 7 glass) will reflect 4% at each surface. In the case of fiber-to-fiber coupling using two ball lenses, the total on-axis transmission through the four lens surfaces would be only 85%. For a material with an index of 2, the loss would be more than 11% per surface on-axis. For fiber coupling using two ball lenses, this would represent an insertion loss of more than 2 db. AR coatings are required to lower these losses.

To grasp how an AR coating works, it is first necessary to understand the wave phenomenon of interference. Figure 3a shows the two extreme cases of interference. When two identical waves that are exactly in phase overlap, the result is constructive interference. The resulting wave has an amplitude equal to the sum of the original two waves. If the two waves are exactly one half wave (or 180) out of phase, then destructive interference occurs; they cancel out and the result is nothing.

If an optical surface, coated with a thin layer of material, has an index of refraction that is higher than air but lower than that of the substrate, there are two reflected lightwaves. One lightwave is from the air/coating interface and the other is from the coating/substrate interface (see Fig. 3b). If the distance the lightwave reflected from the coating/substrate interface travels before being recombined with the lightwave reflected from the air/coating interface is exactly one half of a wave, then destructive interference occurs. The effect of this interference is to suppress reflection and thereby enhance transmission. This effect is the basis of an AR coating.

To get complete destructive interference in the example just cited, two conditions must be met. First, the total optical path length traveled through the coating (double pass) must be exactly one half-wave. This means that a single-layer coating can provide best performance at only one wavelength and angle of incidence. The second requirement is that the amplitude of the two reflected waves must be equal. For this to happen, the index of the coating must be exactly the square root of the index of the substrate.

Unfortunately, there are no useful coating materials that meet this condition for the bulk of optical glasses, which have indices in the 1.5-to-1.9 range. The most commonly used material for single-layer AR coatings is magnesium fluoride (MgF2). With an index of approximately 1.38, this material yields single-layer coatings with a reflectivity of about 1.25% per surface on low-index substrates. Achieving substantially lower reflectivity (<0.25%) over a wide range of both wavelengths and incidence angles requires coatings that consist of multiple layers of varying thickness, composed of at least two materials.

Coating technology

Manufacturing the type of multilayer AR coating just described requires the ability to tightly control the thickness and uniformity of each layer, as well as the index of refraction of these deposited layers. An AR coating in the 1.3- to 1.5-nm range typically requires layers with a physical thickness of only a few hundred Ångstroms; the thickness of these layers must be controlled to within a few percent. Even minute changes in material microstructure can influence refractive index and degrade the performance of the coating. Good adhesion and layer integrity is also important if the optic is to be environmentally durable. Furthermore, economics dictate the use of production equipment that allows large batch sizes and short cycle times.

The most well established and commonly used technology for producing such coatings is evaporation. In evaporation, the parts to be coated are held in movable racks inside of a chamber that is pumped out to achieve a very high vacuum (10-6 Torr or better). Various materials are then evaporated in turn to build up as many different layers in the coating as are required.

Because of the low pressure in the chamber, the mean free path of the evaporated atoms or molecules is several meters. They stream out and re-condense onto any surface in the chamber that has a direct line of sight to the source, meaning that the rate at which the coating material is deposited on the optical surfaces is highly dependent on their distance from the source as well as on their relative angular orientation.

Because of the dependence on the angular orientation of the part, evaporation is best suited for coating planar optics. This method is not suitable for optics with high curvature. Coating highly curved optics by evaporation leads to nonuniform, soft, nondurable coatings.

Since the evaporation technique has been in use for many years, it is a reliable method for manufacturing coatings on a production basis. But it does have two serious drawbacks when applied to ball lenses. First, the high curvature of ball lenses makes it impossible to coat their entire surface uniformly (because the center and edge of each lens have a significantly different orientation with respect to the coating source). Second, since evaporation only allows one side of the part to be coated at a time, coating the entire ball lens requires two coating runs. The tooling commonly in use for holding parts covers slightly more than half the sphere, resulting in an uncoated stripe that runs around the entire circumference of the finished part. Therefore the tiny ball lenses must be precisely oriented during the assembly process to ensure that the right part of the coated surface is facing correctly. Most manufacturers provide a removable orientation dot to aid in this process.

Better alternative

Because of nonuniformity problems, it is at best difficult to produce high-performing, multilayer AR coatings on ball lenses by evaporation. For this reason, the spectral performance of evaporation-coated ball lenses has, in many cases, been less than optimal. Coating uniformity problems, together with the time and trouble associated with performing the required orientation (and subsequent removal of the orientation dot) on such minute parts are a major factor in limiting the use of ball lenses.

However, a form of low-pressure chemical vapor deposition (LPCVD), called IsoDyn, is suitable for producing optical coatings. LPCVD is an established technology in the semiconductor-processing field, where it is used to produce thin films during integrated circuit production. Until recently, the technology had never been used for manufacturing optical thin films.

In the IsoDyn process, the coating material is created through the chemical reaction of a precursor gas at the surface of the substrate, instead of being evaporated or sputtered from a target consisting of the material itself. Specifically, parts to be coated are put into an evacuated chamber and heated to about 500C. The chamber is then filled with a chemical vapor at relatively high pressure (usually 0.1 to 5 Torr). The heat causes a chemical reaction in the precursor gas, resulting in deposition of the desired substance on all exposed surfaces of the substrate. This process is repeated with various precursors to produce a multilayer coating.

Because of the gas pressure, the mean free path for molecules is very short. Therefore deposition occurs at the same rate on every surface within the chamber, regardless of its position or orientation, making IsoDyn technology particularly useful for producing highly uniform coatings on parts with unusual shapes or large curvatures such as ball lenses.

With IsoDyn, surfaces do not have to be in a line of sight with a material source to be coated, so the entire volume of the chamber can be filled with parts, resulting in higher throughput and lower production cost. Economy is further improved because all surfaces of a part can be coated in a single run. Because of the very high penetrating power of the precursor gas, there is virtually no detectable uncoated area on the lens. This combination of film uniformity and complete surface coverage completely eliminates the orientation problems experienced with evaporative coating of ball lenses.

The high temperature used in the IsoDyn process also gives rise to extraordinarily durable coatings. Higher temperatures mean that the molecules are more energetic. This energy causes the molecules to pack more tightly during deposition, resulting in a denser film than can be achieved through evaporation. The overall result is coatings that can survive repeated handling and abrasion and that perform well over a very large ambient temperature range.

A range of ball lenses based on the IsoDyn process is now avaliable for telecommunications. These lenses are offered in materials with a wide range of refractive index, including BK 7, spinel, sapphire, LaSF N9, LaSF N18, LaSF N35, and stabilized cubic zirconia (which has an index of 2.1 at 1550 nm). Standard ball lenses of this type range in diameter from 0.5 to 3 mm. The multilayer IsoDyn coating on these ball lenses delivers less than 0.25% reflection per surface at either 1310 or 1550 nm; a dual-wavelength AR coating is also available. Other wavelength combinations--such as 980 and 1310 nm--and attenuating coatings are also available.

A plot of the transmission of an LaSF N9 lens with a dual-band (1310 and 1550 nm) AR coating is shown in Figure 4. Note that the transmission at 1310 and 1550 nm is greater than 99.5%, which demonstrates a reflection per surface of less than 0.25%.

Ball lenses are a mechanically simple and an economically attractive optical solution to a number of fiber-coupling and collimating problems. The development of a mature coating technology for ball lenses removes the primary impediment to their utilization in many telecommunications applications. u