Why complex modulated optical signals?
by Stephanie Michel
New data centers are being built across the globe, while the latest generation of CPUs introduces a new era for high-performance computing servers. With an order of magnitude more CPU power and RAM and a decrease in latency, it's no problem to map immense amounts of data spread over several servers within a fraction of a second.
Today, data mining on a large scale seems to be reserved for the bigger players who have their own data centers to analyze the big collections of structured and unstructured data, for example, to do marketing focused to individual customer interests. But the infrastructure is now in place for medium-sized or smaller enterprises to also store and analyze big data in the cloud to optimize supply chain, marketing activities, and more. Little businesses that can't afford their own servers can now benefit as well from ultra fast data analytics anywhere at minimum cost by using cloud services.
What does that have to do with fiber-optic networks? Well, while data centers may be well prepared for this data revolution, the more critical question is whether the infrastructure outside can keep pace. Explosively growing amounts of data have become an enormous challenge for backbone networks. For fiber-optic networks not to become the bottleneck of the future, their bit-rate efficiency needs to increase. Very soon, it'll be necessary for fiber-optic infrastructure and signal concepts to support data rates of 100 Gbps and beyond, which will be a problem for traditionally applied data coding schemes.
Benefits of complex modulation
Optical data transport started out like its electronic counterpart, with the simplest and therefore cheapest digital coding schemes: return-to-zero (RZ) or non-return-to-zero (NRZ) on/off-keying (OOK). The signal is ideally a rectangular sequence of ones (power on) and zeros (power off). But this concept faced a limitation when transfer rates reached 40 Gbps.
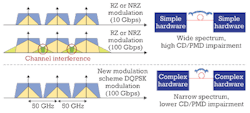
Due to the high clock rate at 40 and 100 Gbps, the bandwidth occupied by the OOK signal becomes larger than the bandwidth of a 50-GHz ITU channel. As can be seen in Figure 1, spectrally broadened channels start to overlap with their neighboring channel and the signals are shaped by the wavelength filters, resulting in crosstalk and degradation of the modulated information.
For this reason, we have to turn our back on OOK and move to more complex modulation schemes such as differential quadrature phase shift keying (DQPSK) for high-speed transmission. Complex modulation reduces the required bandwidth, depending on the symbol clock (baud) rate and enables higher data rates to be transmitted in the 50-GHz ITU channel plan.
These new concepts also support compensation for chromatic dispersion (CD) and polarization mode dispersion (PMD) via signal processing when paired with coherent detection, which provides complete optical field information. Dispersion – an effect caused because lightwaves travel at different speeds depending on their frequency and polarization – leads to pulse broadening that degrades the signal if not compensated. Dispersion is especially an issue for long fiber spans.
The use of coherent detection means that complex optical modulation releases us from the need for PMD compensators or dispersion compensating fibers and from the increase in latency these elements induce.
Complex modulation schemes improve spectral efficiency by using all the parameters of a lightwave for encoding information: amplitude and frequency or phase. Radio engineers have profited from this approach for many years; now it can be leveraged in the optical world.
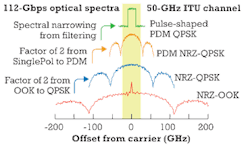
In addition to coherent detection, complex modulation schemes can be combined with other transmission methods to transmit a data signal more efficiently over a fiber link. For example, in polarization division multiplexing (PDM), a second lightwave signal, which is polarized orthogonally to the first, carries independent information and is transmitted over the same fiber (see Figure 2). That's like adding a second channel and doubles the transmission speed without the need of a second fiber.
Other types of multiplexing (like WDM) continue to be used. The use of pulse-shaping filters, which reduce the bandwidth occupied by the signal, completes the toolset.
Figure 3 gives an idea of how a combination of these different techniques can improve spectral efficiency. At the bottom is the simplest scheme: OOK. Using quadrature phase-shift keying (QPSK) instead, the transfer rate can be doubled at the same symbol rate as in OOK, because in QPSK 2 bits are encoded in one symbol. Another factor of 2 can be gained through PDM. QPSK plus PDM enables the transfer of 2 × 2 = 4 times more bits at the same time, meaning at the same clock rate. In the end, after further narrowing the occupied spectrum with a pulse-shaping filter, 100 Gbps can be transmitted in a 50-GHz channel.
No more limits to spectral efficiency?
It would be perfect if we didn't face any further problems in the pursuit of ever-growing data throughput. But of course and unfortunately there are limits.
In the 1940s, American mathematician and electronics engineer Claude Shannon, the "father of Information Theory," found that in any communication channel the maximum speed at which data can be transferred without errors can be described in dependence of noise and bandwidth. He called this maximum bit rate "channel capacity," which is largely known today as the "Shannon limit."
The Shannon-Hartley theorem states:
Channel capacity: C = B log (1 + SN ),
where B is the bandwidth measured in hertz, S the average received signal power in watts, and N the average noise power in watts.
The channel capacity can be increased by either increasing bandwidth or optimizing the signal-to-noise ratio (SNR = S/N). In fact, the theorem provides a theoretical maximum without giving any information about which signal concept gets us closest to this limit.
In practice, SNR is the fundamentally limiting factor. It is and will be the subject of ongoing optimization efforts because, for data rates beyond 100 Gbps, a better SNR performance is needed for long distances to reach the Shannon limit at a given bandwidth.
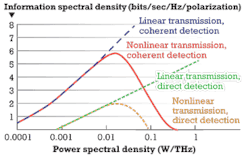
Andrew Ellis, Jian Zhao, and David Cotter took example parameters to simulate the information spectral density C/B in dependence of transmission and detection type (see Figure 4). For nonlinear transmission, the information spectral density does not grow infinitely with launch power spectral density. Due to saturation effects of the power amplifier and nonlinear effects in the fiber itself, there's a maximum value of information spectral density. That would not be the case if the transmission media were completely linear.
In this graph, we can clearly see that direct detection as used in OOK – where information is extracted from amplitude only – can't compete with coherent detection of complex modulated signals in terms of information spectral density.
Also, there's no doubt that the different types of complex modulation have a fundamental influence on how close we get to Shannon's limit of spectral efficiency. But let's step back to first understand the basics of coding and modulation schemes in our next article, "Complex coding concepts for increased optical bit transfer efficiency" (appearing at Lightwave's website).
(Editor's Note: "Why complex modulated optical signals?" is the first in a series of tutorial articles on high-data-rate communications.)
References
- Cisco Visual Networking Index.
- A.D. Ellis, J. Zhao, and D. Cotter, "Approaching the Non-Linear Shannon Limit," Journal of Lightwave Technology, Vol. 28, No. 4, Feb. 15, 2010.
- T. Pfau, X. Liu, S. Chandrasekhar, "Optimization of 16-ary Quadrature Amplitude Modulation Constellations for Phase Noise Impaired Channels," ECOC Technical Digest 2011.
- R. Schmogrow, et al., "Error Vector Magnitude as a Performance Measure for Advanced Modulation Formats," IEEE Photonics Technology Letters, Vol. 24, No. 1, Jan. 1, 2012.
- Figures in this article are contributed by Oliver Funke, Stephanie Michel, and Dr. Bernd Nebendahl.
STEPHANIE MICHEL is technical marketing engineer in the Digital Photonic Test Division of the Electronic Measurements Group at Agilent Technologies.
Past Lightwave Issues