How to detect complex modulated optical signals
We saw in the last part of this series, "An Optical Transmitter for Every Need," how the use of complex optical modulation schemes affects the transmitter architecture. It is not surprising that on the receiver side, we have to rethink the traditional concepts, too.
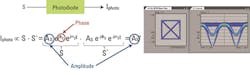
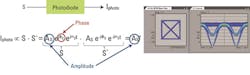
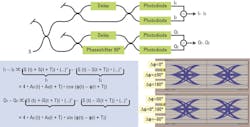
In on/off keying (OOK), we are able to detect the signal simply with a photodiode, which converts the optical power into an electrical current IPhoto. The photocurrent IPhoto originating in the photodiode is directly proportional to the product of the optical signal S and its complex conjugate S*. In the equation in Figure 1 you can see that the result only contains the amplitude AS. IPhoto does not provide any information on the angular frequency ωs and the phase φs. Thus, the QPSK signal in the time domain on the right side cannot be directly mapped to the IQ diagram on the left without ambiguity. You can only tell that the lower curve passing zero represents the diagonal transitions between the four constellation points and the middle curve the outer transitions. The flat signal through 1 represents the cases where the phase does not change, meaning that a symbol is followed by the same one.
For unambiguous identification of the symbol transitions, we have to look for more sophisticated methods that enable detection of the complete electric field including phase information.
Complicating the problem is the fact that in today’s optical communication systems we operate at wavelengths in the near infrared – for example, at 1550 nm, corresponding to a frequency close to 200 THz. So the changes of the electrical field in time and space are several orders of magnitude too fast to be processed with available electronics operating in the MHz to GHz range.
A local oscillator helps
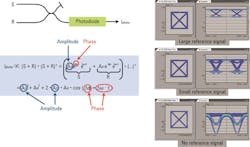
The key to solve both problems lies in measuring not the absolute phase but the phase relative to a known reference signal. In Figure 2 you can see the basic detection setup; the ideally monochromatic laser that produces the reference signal R is often referred to as the “local oscillator.”
QPSK signal mixed with different reference signals.
The signal of interest S and the reference signal R are superimposed in an optical combiner and detected with a photodiode. IPhoto is then proportional to the product of the sum of both signals (R+S) and its complex conjugate (R+S)*. The equation in Figure 2 reveals that the result holds the phase difference Δφ = φS - φR and the frequency difference Δω = ωS - ωR. From Δφ, we can now deduce the evolution of φS over time.
The reference frequency ωR is chosen close to ωS so that Δω is now small enough to be electronically processable.
The phase-dependent term is called the heterodyne term or beat term because it results from mixing or “beating” the two signals.
There is also a term containing the squared amplitude that has no implications as long as only the phase is modulated and the amplitude stays constant - which is the case in QPSK modulation.
At the bottom of Figure 2 we have the case without reference signal, discussed before, with only the AS2 term.
When a reference signal is added that is large in comparison to the signal itself, we see basically the beat term shifted upwards by AR2. It would be advantageous to get only the beat term without this shift.
Suppressing phase-independent terms with a balanced receiver
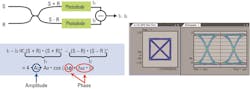
As shown in Figure 3, we can suppress all other phase-independent terms with a balanced receiver. Here, the signal to be detected S and the reference signal R are summed on one branch and subtracted on the second branch of a 2x2 optical combiner (which could be a fiber optical or free-space optical coupler). Each of the resulting signals is detected by one photodiode. The difference between the two photocurrents is then used. In the equation, also given in Figure 3, we can see that all other terms have cancelled out, and only the beat term remains.
An additional advantage of balanced detection is visible as well: the net photocurrent has doubled.
Taking the concept to the IQ plane – IQ demodulator
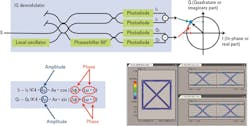
To recover both amplitude and phase, a coherent receiver should provide the in-phase (I) component and the quadrature (Q) component as two separate output signals. For this purpose, we need a second balanced detector. A single local oscillator provides the reference signal for both of them but the phase must be shifted by π/2 to obtain the Q part. Figure 4 gives, for the case of a QPSK signal, an idea of the whole setup, which is called an “IQ demodulator.”
on amplitude and phase.
This setup only works for coherent signals that are not polarization-division multiplexed. In addition, the signal only mixes with the component of the local oscillator signal with the same state of polarization at the detector.
Extending the concept to dual polarization
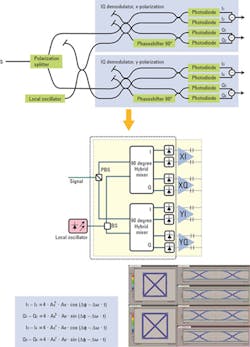
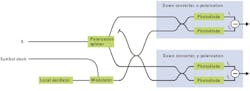
For dual polarization, we have to further develop the demodulator concept. The basic principle stays the same: after a polarization splitter, we now have two IQ demodulators, one for the x-polarization and the other one for the y-polarization. Only one local oscillator provides the reference signals for all branches.
The block diagram is given in Figure 5. You can see that there are four output signals to resolve I- and Q-coordinates, one for each polarization direction respectively. In the equations the upper indices h and v reflect the horizontal and vertical polarization state of the signal with respect to the polarization reference frame of the receiver. This polarization diversity architecture also assures that all of the signal is mixed with the local oscillator, regardless of the input state of polarization. Therefore it is commonly used, even if the signal does not use dual polarization.
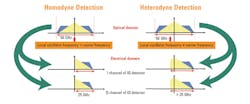
So far, we have investigated receivers with a local oscillator of a frequency ωR that is different from the signal’s frequency ωS. These are called heterodyne receivers.
In homodyne receivers, the local oscillator has the same frequency as the carrier signal itself. The advantage: the above terms are not frequency dependent anymore.
Figure 6 quantifies the required electrical bandwidth for both homodyne and heterodyne receivers. For homodyne detection, where the local oscillator has the same frequency as the signal itself, half the signal’s optical bandwidth is needed. For a heterodyne receiver the needed electrical bandwidth increases with the frequency offset between local oscillator and signal.
frequency offset between signal and its reference.
Use a delayed copy of the signal as a reference – delay-line interferometers
After what we have seen, it seems that a local oscillator is indispensable for recovering the phase information. How about overlaying the signal with a copy of itself? This way, we also get a reference signal where ωR = ωS.
One could think that this effort is not very promising because it may not be clear how to gain additional information on the phase that way. But this self-homodyne approach is useful because we are interested in detecting the phase change over time. So, if you split the signal in two and overlay the signal with the delayed copy as a reference signal you get information on the phase changes.
The advantage of this measurement method is that it is not subject to inaccuracies due to slow (in comparison to the symbol rate) frequency fluctuations of an external local oscillator and of the carrier laser itself.
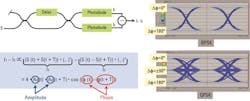
This kind of receiver setup is known as a delay-line interferometer. Figure 7 shows a balanced delay-line interferometer with the signal S(t) and the signal S(t+T) delayed by T.
The equation here shows that the result is dependent on the cosine of the phase difference between the original signal and its delayed copy. Due to the periodicity of this function, only phase differences between 0 and π can be uniquely identified and only for delays T that are approximately an integer multiple of the carrier period 2π/ωS. This is sufficient for BPSK but for phase recovery of QPSK and higher-order modulation schemes, we have to add another delay line interferometer phase shifted by π/2 relative to the other delay-line interferometer to cover the full phase range from 0 to 2π.
Figure 8 shows the setup with an additional delay-line interferometer for receiving the two independent I and Q components. Q1-Q2 is measured additionally, while I1-I2 stays unchanged.
Analogous to a heterodyne receiver, the delay-line interferometer can also be expanded for polarization-sensitive measurements.
With a delay-line interferometer, we don’t need an external local oscillator and therefore don’t have to deal with oscillator-introduced phase noise; we also require less signal processing. However, this approach does have disadvantages that still might lead us to prefer a heterodyne receiver.
First, to measure phase changes over time with a delay-line interferometer without clock data recovery (CDR), the delay and the sampling period need to be considerably smaller than the symbol period. Today’s symbol rates have reached a level where this can be hard to accomplish. In addition, for low-power signals the measurement sensitivity is reduced because the reference signal is also of low power and suffers from noise accumulated on the transmission link. For implementation with a sampling technique, the measurement time increases and a trigger is required. Bottom line, a homodyne receiver is not very flexible.
Until now, we have exclusively been looking at time-domain detection techniques. Alternatively, we could also detect the frequency spectrum and deduce from it via Fourier transformation the time-domain signal.
Frequency-domain detection
To recover a complex modulated optical signal from its spectrum, we have to measure the complex spectrum, meaning with amplitude and phase information.
This can be performed with a complex spectrum analyzer that separates the different optical frequency components with a dispersive element. All the frequency bands can either be detected simultaneously with multiple detectors or sequentially with a scanning narrow-band optical filter and a single detector.
For recovering phase and amplitude, we again employ a local oscillator as a reference signal. For recovering both components, we need a source emitting at two optical frequencies.
Figure 9 shows the complete setup that is needed to measure the polarization-resolved complex spectrum.
The big plus of frequency-domain detection is its virtually unlimited bandwidth, meaning also unlimited time resolution. The bandwidth depends on the sweep range of the local oscillator so that we can reach bandwidths in the THz range with today’s tunable external cavity lasers. The other big advantage is that we don’t need a high-speed receiver.
On the other hand, there are also major drawbacks.
For example, it is only applicable to periodic signals because these result in the required discrete spectral peaks. Additionally, we now need a symbol or pattern clock. The precision of the recovered time-domain signal directly depends on the spectral resolution that determines the number of sidebands that can be resolved. The spectral resolution that can be reached today limits the pattern length to a few tens of symbols.
These factors and the fact that this method does not give results in real time, make frequency-domain detection inapplicable for network receivers. In fact, we would have to deal with long measurement times and fairly complex measurement setup and signal processing.
Finally, in frequency detection, all non-periodic effects are averaged out. This is also true for polarization-mode dispersion (PMD), which therefore cannot be compensated.
Preferences?
Self-homodyne setups need little signal processing and are the least sensitive to phase noise. Still, they are not very flexible, work only close to the design symbol rate, and are less sensitive than heterodyne implementations.
The heterodyne time domain detection methods offer the highest flexibility. Unlike frequency-domain detection, they can be used for real-time detection. They therefore are applicable to live signals in data networks. Equivalent-time sampling only works for repetitive signals of a limited length, for example in test and measurement scenarios.
With real-time sampling, we can reconstruct the complete signal in all domains and without limitations regarding the modulation format. Neither do we face any limitations regarding signal length in heterodyne time-domain detection. PMD and CD can be compensated during signal processing. In this case, only the signal processing is the throughput limiting factor.
At the same time, we have to be aware that we need four-channel high-speed equipment for this approach, such as a high-performance real-time digitizer with very low jitter and noise and a high effective number of bits (ENOB) over the whole frequency range.
We’ve now covered the basic concepts of constructing a receiver. In the next part of our series, we‘ll have a look at the details of a time-domain real-time sampling setup.
References
1. Block diagram from “OIF Implementation Agreement for Integrated Dual Polarization Intradyne Coherent Receivers.”
All other figures in this article are contributed by Oliver Funke, Bernd Nebendahl, and Bogdan Szafraniec.
Stephanie Michel is technical marketing engineer in the Digital Photonic Test Division of the Electronic Measurements Group at Agilent Technologies. The Electronic Measurements Group will spin out of Agilent in November 2014 under the name Keysight Technologies.