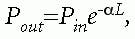Enabling those next-generation optical networks with new system technology
One of the most promising solutions to the limitation of long-haul transmission is the use of high-gain forward error correction in a system.
SIMON KEETON, SATISH SRIDHARAN, and MICHAEL JARCHI, Vitesse Semiconductor Corp.
When deploying the next-generation long-haul optical transport networks, carriers are driven by the imperative to support unprecedented growth while at the same time dramatically reducing the cost of the network. The overall goal of the long-haul network is to move the most data from the originating point to the terminating point, using the fastest possible method with the most reliability in the most inexpensive manner.
Increasing bandwidth in a system can be approached in many ways. Two of the most popular are increasing the line rate and increasing the number of channels sent on a single fiber. Increasing the line rate of the system involves the use of time-division multiplexing (TDM). When using TDM, more data is sent in the same amount of time by allocating less time for each individual bit that is sent. Common line rates for existing systems are based upon SONET/SDH transmission rates of OC-48 (2.5 Gbits/sec), OC-192 (10 Gbits/sec), and the emerging line rate of OC-768 (40 Gbits/sec). Unfortunately, increasing the line rate in this manner has a price. Not only is the complexity increased greatly in terms of the components associated with the transmission, but also the properties of the fiber and the signal degrade at the higher line rates.
Without a method to work in a more degraded environment, transmission at the higher line rates can be very complicated. Increasing the channel count-or in networking terms, performing WDM-can also increase the capacity or bandwidth of the system. By using different frequencies to transmit independent channels of information, the overall bandwidth is substantially increased. Again, there are limiting factors to WDM transmission that involve the degradation of signal transmission quality. Without a method to work in a more degraded environment, transmission through the use of WDM can be limited.
Removing cost from a system can be approached in many ways. One of the more effective ways to remove cost is to remove as many conversions from the original transmission medium as possible. In the case of optical networking, that means the removal of conversions from the optical domain to the electrical domain.
In many cases, these conversions take the form of a regenerator, which performs an optical-electrical-optical (OEO) conversion, typically receiving a severely degraded incoming optical signal, and transmitting a new optical signal in a form in which the amplitude, waveform, and timing characteristics of the signal are back to optimal levels to conform to specified network limits. Removing these regeneration points from a long-haul network can significantly reduce cost, although the removal of such regenerators can have a significant detrimental effect on the overall signal quality. Without a method to work with an errored signal, removal of the regenerator is next to impossible.Ultimately, the design of the long-haul transmission system rests upon the ability to deliver a system that meets predetermined requirements for quality. As indicated, the goals of increasing bandwidth and reducing cost can be limited by degradations of the signal itself. There are many approaches to counter these degrading effects, including developments in the fiber itself, the optics, amplifiers, and optoelectronic products.
In addition, one of the more promising solutions to the limiting issues with long-haul transmission is the use of forward error correction (FEC) in a system. FEC has the ability to detect and correct errors incurred during transmission. This ability to detect and correct errors means that the overall quality of the delivered service is maintained even when the transmitted signal itself is severely degraded.The ever-increasing need for bandwidth has consistently pushed the limits for transmission rates. Current solutions for long-haul networks typically run at SONET/SDH rates of OC-48 and OC-192. Soon to be available however, will be components to support the next transmission rate of OC-768. It is expected that equipment providers will have complete OC-768 solutions as early as this summer.
As providers move toward these higher transmission rates, it also becomes imperative to send the signals further without the use of OEO conversions, significantly reducing cost. Unfortunately, as systems evolve to higher data rates and longer distances, limiting effects such as chromatic dispersion and attenuation play a larger role.
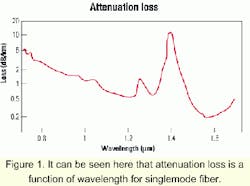
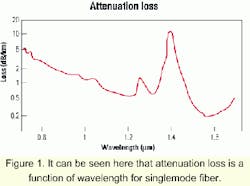
One of the limiting effects in a long-haul transport system is signal attenuation. Attenuation is the decrease in power of an optical signal as it travels through fiber. The effect of attenuation can be modeled as follows:where Pout is output power at the end of the fiber, Pin is input power at the fiber, a is fiber attenuation, and L is fiber length. Often the loss due to attenuation is specified in dB/km, and a curve is provided for various fibers. Attenuation loss as a function of wavelength for singlemode fiber is shown in Figure 1. Not surprisingly, it can be seen that the curve has minima at common communication wavebands of 1,310 nm and 1,550 nm.
In long-haul communication systems, a central wavelength of 1,550 nm is commonly chosen due to the low attenuation loss. As a simplified example, an environment with a loss of 0.25 dB/km and a "span budget" of 23 dB means a travel distance of 92 km. Decreasing the attenuation loss factor and/or increasing the span budget can have a significant impact on the ability to transmit signals further.
The effect is the pulse received at the end of the fiber is wider than the original pulse and can overlap adjacent bits. If the spreading is excessive, it becomes harder to distinguish individual bit pulses. This phenomenon is commonly referred to as intersymbol interference (ISI). An increase in ISI is reflected in terms of a degraded signal (increased bit-error rate).
In addition to attenuation and chromatic dispersion, there are hosts of other limiting factors, including nonlinear effects such as self-phase modulation, cross-phase modulation, and four-wave mixing. Many of these limiting factors are inter-related. The bottom line for the network architect is that these limiting factors have to be taken into account when planning the long-haul network.
In general, these limiting factors mean additional errors or "noise" in the system, where the network architect is trying to reduce the unwanted noise and increase the level of the original signal to be transmitted. FEC can be used to counter these effects by detecting and correcting the errors induced into the system by these limiting effects.
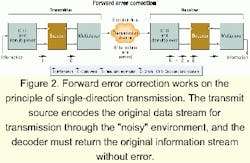
The use of coding schemes for reliable transmission and storage is well understood. In fact, pioneering work by C.E. Shannon was published in the late 1940s. All coding schemes rely upon the same general principle of taking the original information stream and encoding the information to allow the newly encoded information stream to endure an environment where noise would adversely affect the transmitted signal. The encoded information stream is eventually decoded, with the optimal result being the exact replication of the transmitted signal at the receiver without any errors induced by the environment it passed through.FEC works on the principle of single-direction transmission (see Figure 2). The transmit source encodes the original data stream for transmission through the "noisy" environment, and the decoder must return the original information stream without error. There is no feedback from the receiver to the transmitter to indicate errors and ask for retransmission. With FEC, all detection and correction of errors occurs at the receiver.
The use of FEC in fiber-based systems was originally targeted for undersea applications where the reliable transport of information over long distances was paramount. Advancements in coding schemes and standardization led to the release of an International Telecommunications Union (ITU) standard for FEC for undersea systems in 1995, ITU-T G.975, or what is commonly referred to as G.975 FEC. This code utilizes a Reed-Solomon (RS) linear block code-RS(255,239)-that incurs about 7% additional overhead in it's use.
Performance of a code can be defined in many ways. The most valuable criterion for evaluation is the error-correcting performance of the code (for a given additional overhead "cost"), which can be expressed as the relationship between bit-error rate (BER) after FEC correction and BER before FEC correction. This relationship can also be described in terms of coding gain, which is the difference in the input optical power of the receiver required for coded and uncoded operation to provide a specified level of communication performance, usually stated in terms of BER.
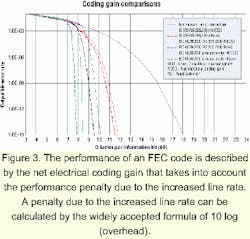
Reed-Solomon codes are "out-of-band" FEC codes where additional information helpful to the detection and correction of errors is appended to the original information. Due to this increase in information, out-of-band codes increase the line rate of the transmitted signal from its original rate of transmission. This increased rate of transmission introduces a performance penalty (from the increased line rate), consisting of a noise penalty due to wider bandwidth receivers and eye closure caused by greater dispersion due to the increased line rate.The performance of an FEC code is described by the net electrical coding gain (NECG), which takes into account the performance penalty due to the increased line rate. A penalty due to the increased line rate can be calculated by the widely accepted formula of 10 log (overhead). As an example, for the RS(255,239) G.975 code, the penalty in coding gain can be calculated as 10 log (1.0669), which results in 0.28 dB. The G.975 code has a raw gain of ~6.3 dB and an NECG of ~6 dB (6.3 dB - 0.28 dB) at an output BER of 10-15 (see Figure 3).
As of late, the application space for the G.975 FEC code is changing rapidly. The emergence of a new standard for optical transport networks (G.709 defines the optical network-to-network interconnect) that utilizes the G.975 FEC code is greatly increasing interest in FEC as a standard for network-to-network interconnect and as a universal transport standard. At the same time, the use of G.975 FEC in long-haul systems is starting to fade. For the long-haul-system environment, performance of the network link is of paramount importance. In these applications, stronger codes with superior performance to G.975 FEC are taking a leadership position.
Codes can be divided into two different categories: block codes and convolutional codes. Block codes divide the incoming data stream into blocks of data and append additional information to these blocks to help the decoder detect and correct errors. In this manner, block codes depend only on the current data stream running through the system. Convolutional codes, on the other hand, rely not only on the blocks in the current data stream, but also on data in previous blocks. In this manner, convolutional codes require memory. Designing a high-performance convolutional encoder/ decoder to operate at high data rates is difficult, so the majority of coding schemes used in optical networks today use block codes.
Block codes use modulation and demodulation techniques for transmitting and receiving the data. Most common in optical networks is the use of binary encoding and decoding, where information is quantified into two discrete output symbols (1,0). These codes are described as hard decision codes.
Alternate approaches use more than two discrete symbols for demodulation-it is said these systems make soft decisions. An example is a system that would make decisions based on a "hard 1," "soft 1," "hard 0," or "soft 0," giving four discrete output symbols. Soft decision circuits can offer significant performance advantages over traditional hard decision circuits, but are much more complicated to implement.
As previously indicated, Reed-Solomon codes are widely used in optical systems today. The G.975 RS(255,239) code uses a hard decision code for a memory-less channel, hence a block code. Many people are investigating the use of stronger codes for optical systems. One approach is the use of concatenated code (see Figure 4), where several small codes are embedded within one larger outer code.
Using two different types of codes enables the decoder to correct different types of errors. For instance, a Bose, Chaudhuri, Hocquenghem (BCH) (239,223) code can be embedded with
the standard Reed-Solomon code RS(255,239). The incoming data is assembled into blocks consisting of 223 bits, and these blocks are encoded to form a 239-bit BCH code word. Eight such 239-bit BCH code words can then be assembled together to form the information vector for the RS(255,239) code word.
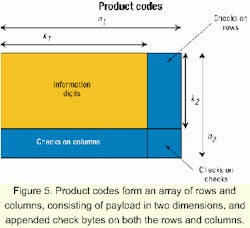
In this approach, there is an inner and outer code employed at both the encoder and decoder. Concatenated codes are reasonably effective for both burst and randomly distributed errors and have the benefit of being able to just use the outer RS(255,239) code for compatibility with systems that use the same G.975 RS(255,239) code. The overall performance of the concatenated codes, however, does not meet the performance standards of other useful codes such as product codes.Product codes have the unique characteristics of not being a single-dimension code as well as allowing iterative decoding in the two dimensions. Product codes form an array of rows and columns (see Figure 5), consisting of payload in two dimensions, and appended check bytes on both the rows and columns.
The general operation consists of checking all rows, then all columns for correctable errors. Anything that can be corrected is corrected, and the process is repeated. Previously uncorrectable errors now become correctable after successive correction sweeps. By evaluating the number of iterations needed, it is possible to deliver excellent random error-correction performance in a reasonable amount of processing time (latency). By an appropriate choice of codes, a good degree of burst error-correction performance can be achieved.
The performance of the above-mentioned codes, in addition to the use of no FEC, is shown in Figure 6, from a view of input BER vs. output BER. Without FEC, the output BER is simply the input BER. With RS(255,239) FEC, an output BER of 10-15 can be achieved from an input BER of 8x10-5. With a RS(255,239)-BCH(239,223) concatenated code, an output BER of 10-15 can be achieved from an input BER of 1.4x10-3. With a BCH(255,239) product code, an output BER of 10-15 can be achieved from an input BER of 7x10-3. The product code is the best performing code, detecting and correcting the most severely errored input signal for a given overhead cost. These BER curves can also be shown in the form of an optical signal-to-noise ratio (OSNR) vs. output BER, which shows that a product code can deliver over 3.5 dB more NECG gain over the traditional G.975 RS(255,239) code and 1.7 dB over concatenated codes with similar overhead.
Optical networks are continually pushing the limits to transfer the most amount of bandwidth in the most cost-effective manner. Networks have been evolving through the use of DWDM and by increasing overall transmission speeds. Core networks have evolved significantly over the past two years, moving from data rates of 2.5 Gbits/sec to 10 Gbits/sec and looking forward soon to 40 Gbits/sec.
The impairments of transmission also increase as the transmission speed increases. In many cases, the impairments increase in a nonlinear fashion, even though the transmission rates are increasing in a linear fashion. The same phenomenon is also true for DWDM systems. FEC becomes vital in these systems, giving the network architect another tool to provide reliable transmissions.
The demands of the optical network will continue to focus on more bandwidth for fewer dollars. To help architects deliver these solutions, FEC will continue to be used. At the same time, there is much work being done to deliver a better FEC solution. FEC will be tailored to meet the needs of the 40-Gbit/sec network, where FEC is critical.
Not only is performance a primary concern, reducing the associated overhead becomes more of a necessity. Optics and optoelectronics will limit the data rate that can be supported in a system. FEC algorithms must take these limitations into account to deliver a usable function to the system and network designer. Future advancements in optics and optoelectronics will allow the use of even stronger FEC codes.
The idea of error detection and correction codes is not new-it is only the application of these codes to next-generation optical networks that is innovative. One of the stronger characteristics of FEC codes is their long history of providing a valuable asset in many types of transmission systems.
Simon Keeton is product-line manager at Vitesse Semiconductor Corp. (Camarillo, CA), and Satish Sridharan and Michael Jarchi are senior members of Vitesse's technical staff. They can be reached at the company's Website, www.vitesse.com.