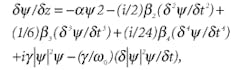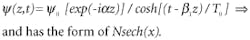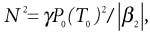Future of solitons

The move to higher transmission speeds has opened the door to solitons. Here's an overview of the technology.

DR. ANDRÉ GIRARD, EXFO

Solitons are light pulses that can propagate in a non-linear dispersive medium with no broadening over very long distances. As a result, they have attracted great interest in the field of communications.

Solitons work because two effects occur in optical fibers that serve to offset each other when properly managed. One is chromatic dispersion, which causes pulses containing a spectrum of wavelengths to spread out as they travel along an optical fiber. The other is called self-phase modulation (SPM), which spreads the pulse spectrum over a broader range of wavelengths. Depending on the mutual relationship between dispersion and SPM, the two can balance each other out, so once the pulse comes to equilibrium in the fiber, it retains its shape or dispersion, and SPM can make the pulse compress or even broaden more severely (see Lightwave, "Handling Special Effects: Nonlinearity, Chromatic Dispersion, and Soliton Waves," July 2000, page 84.).

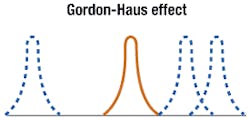
However, attenuation weakens the pulse and consequently fights against maintaining the shape of the pulse along the fiber span. Optical amplifiers have been developed to balance attenuation and maintain pulse shapes. However, optical amplifiers, as is the case with any radiation source, add noise-namely amplified spontaneous emission (ASE) that makes the pulse jitter in the time domain. The fundamental soliton shape (such as sech) has a long tail; if a pulse jitters, its long tail can make it overlap the adjacent pulse, destroying both. This effect is called the Gordon-Haus effect. Erbium-doped fiber amplifiers (EDFAs) typically have large ASE compared to other amplifiers such as Raman amplifiers. So stimulated Raman scattering from the fiber itself can be a good amplifier candidate for restoring soliton pulse strength.

Figure 1. The fundamental soliton is one of the solutions of the non-linear Schrödinger equation.

The self-restoring nature of solitons makes them attractive for high-speed, long-haul transmissions. With transmission speeds now approaching 40 Gbits/sec over increasingly longer distances, the stress on systems is rapidly approaching a critical threshold. Solitons could provide interesting future solutions.

Soliton systems have demonstrated very high transmission speeds in laboratory settings. There was even a time at the very beginning of singlemode fiber-optic transmission when system designers considered the use of solitons for long-haul transmissions. The solitons would be created along the fiber from a pulse train based on return-to-zero (RZ) bit code. But the development of the EDFA, with its high noise, modified this strategy. Network system designers quickly adopted the nonreturn-to-zero bit code as much easier to handle-and that was the end of the soliton business.

Now that we are considering 40 Gbits/sec, interest in RZ is back on again. And with the use of the higher power required by the need to provide higher optical signal-to-noise ratio (OSNR) at that bit rate, nonlinear effects such as SPM and Raman stimulated scattering are being generated. They consequently can be used smartly together with dispersion management instead of trying to avoid them. Thus, the potential for new amplifiers based on this Raman effect is attracting interest. And Raman amplifiers have lower noise than EDFAs.

The door is wide open again for soliton transmissions. We are back at the drawing board, looking at fundamental theory to delineate the challenges and stimulate further research. To accomplish that, we must understand solitons as precisely as possible.

Solitons are well represented by the elegant solution of the nonlinear Schrödinger equation of propagation of an electromagnetic wave in a nonlinear dispersive medium, where the index of refraction of this medium has the form n = n(I, λ). The Schrödinger equation can be represented as follows:

where ψ(z,t) is the pulse signal envelope propagating over the distance z in the time variable t in a frame of reference traveling at the group velocity of the carrier wave. We need to consider the concept of group velocity because we are dealing with a dispersive medium. β₂, β₃, β₄ are the second, third, and fourth order group velocity dispersion (GVD) parameters-or, in other words, the second, third, and fourth derivatives of the wavenumber β (βnk, with k=w/c) as a function of the optical frequency w or wavelength. In principle, there is no limit to the expansion of β to higher orders except that the effect of these orders quickly becomes negligible.

The Schrödinger equation has the great advantage of producing analytical solutions. One of them is:

That solution is called a soliton, and N corresponds to the soliton order. N is defined from the following equation:

where T₀ is the pulse width, Y the non-linear coefficient, and P₀ the pulse power. So we can have soliton transmission when certain conditions of non-linearity, power, pulse width, and dispersion are met.

When N=1, the soliton is called the fundamental soliton. Higher-order solitons are possible.

Another solution, sech²(x) has a narrower spectrum than the sech pulse. Figure 1 illustrates this sech pulse shape.

Figure 2. Equilibrium between non-linear effects and dispersion.

The pulse has a typical narrow width but has a long tail that can be disadvantageous if the pulse suffers a jitter (time domain wobbling or oscillation) and overlaps an adjacent pulse in the time domain. Solitons have the tendency to destruct when they overlap.

Another factor to consider is that solitons are an equilibrium product between chromatic dispersion and nonlinear effects. The chirp induced by non-linear effects cancels the one induced by chromatic dispersion (see Figure 2). This cancellation depends on the relationship between the variation of the pulse phase in the time domain (this is the definition of a chirp) induced by the dispersion and the one induced by the SPM, a nonlinear effect present when the power input to the fiber link is sufficiently high in a sufficiently small core fiber over a sufficiently long length of fiber. The product of β2 (the GVD parameter) and C (SPM-induced chirp) is the key issue here (see Figure 3).

Figure 3. Pulse-broadening factor for different relation between dispersion and self-phase modulation (b2C). (Source: G.P. Agrawal, Fiber-Optic Communication Systems)

As figure 3 illustrates, when the distance of propagation in the fiber is equal to the dispersion length (L_D, the distance at which the pulse starts to severely broaden because of the dispersion), the chirp due to SPM cancels the temporal phase variation due to dispersion, and the pulse does not broaden. This case is illustrated in Figure 2.

Now in dispersion-unshifted fiber where the dispersion is positive (for instance D=17 psec/(nm-km) at 1,550 nm) in the 1,550-nm wavelength range, the GVD parameter β₂ is negative and the dispersion is said to be anomalous. In that case, as the chirp C is always positive, the product of C times β₂ is always negative, and the pulse compresses if the distance of propagation is smaller than the dispersion length L_D. This case is illustrated in Figure 4 by Cβ₂<0 with z/L_D<1.

Figure 4. The Gordon-Haus effect is also called the timing jitter. To maintain power, there is a need not only to amplify, but also to take into account accumulated dispersion and soliton-soliton interference.

When the distance of propagation is longer than L_D, the pulse starts to broaden again. Consequently, by careful management of the dispersion along the fiber span and the nonlinear effects (for instance, the chirp from SPM), the soliton can be maintained in the time domain and avoid having its tail or its shape unacceptably changed. Dispersion and cross-phase modulation would play the same role in a DWDM system.

Figure 5. In an anomalous dispersion regime, pulse distortion and timing jitter are reduced and peak power is enhanced. That constitutes a form of dispersion management.

This phenomenon of dispersion and SPM management can also be found with other transmission codes, such as RZ code, where the bit pulse is short enough. It is also understood that a soliton can generate itself from an RZ pulse, meaning that from this careful management of dispersion and nonlinear effect, the RZ pulse can transform itself into soliton inside the range z <L_D.

The development of successful soliton technologies will depend on the following factors:

The distances in the long-haul networks will continue to increase, especially considering the demand for longer distances between repeaters (ultra-long-haul network).
The bit rate will continue to increase to levels of 40 Gbits/sec with shorter pulses, OSNR increases, and consequently higher transmitter output power, bringing concern for nonlinear effects and dispersion.
New optical amplifiers will be considered with lower noise, higher output power, and longer spans.
Technical development will bring serious consideration for all-optical networks.

The consequences associated with the technical requirements for successful soliton transmissions will be:

The soliton pulse must meet certain conditions, such as special sech shape (this shape has a long tail), and the pulse width and peak power must come to N=1 for a fundamental soliton in:
During soliton-soliton interaction, there must be a separation between neighboring solitons-TB/T0. In other words, solitons must be isolated from one another:

The attraction or separation between neighboring solitons depends on several factors such as relative phase, amplitude, and the soliton separation itself.

To maintain the power in a lossy fiber, solitons need to be amplified, taking into account the accumulated dispersion and ASE.

Solitons are destroyed if L_A>L_D; L_D=T₀²/|β₂|; L_D>200 km; |β²|>1 psec²/km, then L_A=30-50 km. Raman amplification can also be considered as a possible solution to extend L_A.

We need to develop a technology that allows efficient amplification and simultaneously takes into account not only the accumulated dispersion, but also the amplifier ASE so as to avoid the Gordon-Haus effect (timing jitter-see Figure 4):

A solution to soliton destruction is an axial variation of dispersion in the dispersion-compensated fiber (DCF) (|β₂(z)|=|β₂(0)|exp(-αz). DCF generates a frequency chirp through SPM; DCF is not to be applied after soliton amplification, but just before the amplifier.
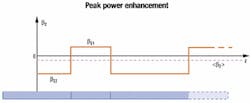
Dispersion management should envision increasing fiber segments as beneficial, as it permits longer amplifier spacing. Dispersion management involves an anomalous regime (β₂<0) that reduces pulse distortion and lowers time jitter (sometimes by three times). That could induce peak power (or energy) enhancement (see Figure 5).

Several challenges remain in the near term that must be addressed before solitons can be applied effectively. For example, practical application of soliton technologies within the telecommunications industry must develop refined control techniques capable of separating solitons by several times their pulse width. We must also master and regulate slight differences in soliton amplitudes. To harness solitons' exceptional transmission speeds, we must be able to create synchronous amplitudes as well as phase modulation with optical filtering.

As soon as these specific issues are resolved, we may indeed look forward to a new generation of transmissions based on soliton waves.

Dr. André Girard is a senior member of the technical staff at EXFO (Quebec City).

Drop us a line
Address letters to:
Letters to the Editor
Lightwave
98 Spit Brook Road
Nashua, NH 03062-5737
e-mail to: [email protected].
Include daytime telephone number.
Letters may be edited.