The Evolution and Implementation of Encryption across Layer 1 Networks

Encryption is in the news these days for lots of reasons. And with each report of the ever-increasing hacks of corporate and government sites, the need for encryption becomes more urgent.

For roughly the last 20 years, network operators have felt that encryption at the higher layers of fiber-optic-based networks would be sufficient when transferring sensitive data. However, hackers have become more experienced and recently have been able to "crack the code" more easily. In response, many data and financial centers now require encryption at Layer 1 in addition to higher layers. This added encryption makes it nearly impossible to decipher data transmitted over the public network.

This practice has become more popular outside of the United States in particular; not surprisingly, financial institutions and government agencies have been quickest to embrace this higher level of encryption. But with the growing occurrence of hacking attacks, U.S. organizations are now finally turning to Layer 1 encryption as well.

Laying a Secure Foundation

What's involved in implementing Layer 1 encryption? An effective strategy covers these key areas:

• Establishing a shared key used by the encryption and decryption algorithm. The data becomes extremely difficult to decode when shared only with the two designated end points, an approach otherwise known as "the secret handshake."
• Allowing a shared key to be transmitted over an insecure communications network. The Diffie-Hellman key exchange was one of the first approaches for this task – a coded message is shared across the network and used to generate an identical key which is nearly impossible to reverse by anyone else.
• Without a reverse operation for modulus calculations, the security stems from the difficulty of calculating the discrete logarithms of very large numbers.
• Additional steps – another layer of "handshaking" between the two end-points – beyond Diffie-Hellman further secures encryption.
  

Let's take a closer look at these elements.

Encryption Algorithm and Key Exchange

The Advanced Encryption Standard (AES) is the most popular encryption and decryption algorithm (see Figure 1). AES went into effect as a government standard on May 26, 2002. AES is the first publicly accessible and open cipher approved by the US National Security Agency (NSA) for top secret information. Use of the standard 256-bit AES algorithm is based on the National Institute of Standards and Technology (NIST) FIPS 140 publication; more on this later.

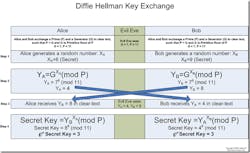
With an algorithm selected, the first step for a secure encryption process is the establishment of a shared key that the encryption and decryption algorithm will use. The important characteristic here is that the key must be extremely difficult to decode and be shared only with the two designated end points. One of the earliest methods for this process is the now widely used Diffie-Hellman key exchange (see Figure 2).

The implementation of the Diffie-Hellman protocol uses a multiplicative group of integers: modulo p, where p is prime and g is a primitive root of modulo p. Since there isn't a reverse operation for modulus calculations, the security derives from the difficulty of calculating the discrete logarithms of very large numbers.

To start the Diffie-Hellman exchange, the two parties involved in the transmission must agree on two non-secret numbers. The first number is g, the generator, and second number is p, the modulus. These numbers can be made public and are usually chosen from a table of known values. g is usually a very small number while p is a very large prime number. Next, each party generates its own secret value. Then, based on g, p, and the secret value, each party calculates its public value. The public value is computed according to the formula: Y = g^x mod p.

In this formula, x is the secret value and Y is the public value. After computing the public values, the two parties exchange their public values. Each party then exponentiates the received public value with its secret value to compute a common shared secret value. When the algorithm completes, both parties have the same shared secret that they have computed from their secret value and the public value of the other party

Applying Encryption in the Real World

In the fiber-optic network environment, operators should look for a line card that performs encryption/decryption over standard optical traffic following the AES-256 specifications. The security technology needs to enable encryption at any of the line rates the line card supports.

This type of encryption process likely would use an AES-Galois/Counter Mode (GCM) core with a 64-bit word-based data interface to implement the block cipher confidentiality and authentication routines. The core can then support various key sizes (GCM = 256, for example), a fixed nonce/initial vector (IV) size of 128 bits, and a fixed length tag (message integrity check or MIC).

The AES-256 core integrates all of the AES and hash functions together with the counter mode (CTR) logic, hash length counters, final block padding, and tag appending and checking features, including external framing circuitry. The frames would then establish a demarcation where frame overhead and collateral system information such as IVs, key update messages, and MICs are passed in the clear while the data itself is encrypted.

The client frames are grouped into cryptographic messages covering 8x510 sixty-four-bit words. Each cryptographic message is processed by the hardware encryption module using AES-256, which provides confidentiality using CTR and integrity using a Galois hash calculation. Overhead is added to the proprietary frame format to allow transmission of a cryptographic IV (12 bytes) and MIC (16 bytes) for each message. The overhead also provides status flags for controlling key changes and reverse indication of MIC and IV replay failures from the receiving end.

The generation of IVs is autonomous in the transmit encryption module. The transmit end inserts the IV into the frame overhead before each message, and the receive end extracts it from the frame for decryption. For GCM, the requirement for each message IV to be unique is met by using a simple counter for the IV, which is reset every time a new key is loaded. Note that IV exhaustion is not possible, as the IV counter size (32-bits) can accommodate data rates up to 14.025 Gbps within the lifetime of the key.

Replay attacks can be detected at the receive end very easily. Because a simple counter is used for the GCM IV, the line card simply rejects any IVs numerically less than or equal to the last successfully received IV for the duration of a link key.

The GCM algorithm requires that data is not forwarded until the MIC is verified. This requires a store-and-forward stage after the line-rate decryption for the entire cryptographic message, since the MIC validation cannot be completed until a short time after the last message data is received.

Bulletproof Encryption

The combination of AES-256 and Diffie-Hellman key exchange is a well-accepted security strategy. But with the increasing sophistication of network hackers, this level of security alone is no longer enough to provide complete assurance. For example, an unknown source could be listening and trying to synchronize with the encryption source.

To prevent such hacking attempts and other malicious schemes, another layer of coordinated handshaking between the two end-points must be created to insure complete privacy of all encryption functions and, most importantly, your private data. Optical transport systems vendors often can make such additional protection available as part of their secure line cards.

Meanwhile, emerging applications will present new security challenges. For example, the emergence of quantum computing will require development of new methods of security, particularly key handling. One of the most recent developments here is "Ring Learning with Errors." Briefly, polynomials with randomly small coefficients are used to calculate and share the secret key. This method is considered not susceptible to quantum computing attacks.

So, one thing we know: Encryption technologies will continue to develop as security continues to get more challenging.

Gene Norgard is vice president of operations at Sorrento Networks. He manages the operations of Sorrento Networks International and is directly responsible for manufacturing, repair, and development of the GigaMux product range. He has been involved with engineering development and manufacturing for more than 30 years, the last 20 as a senior executive. Gene was previously vice president of engineering at Sorrento Networks; prior to that, he was director of engineering at Charles Industries and was a founder and vice president of Oasys Telecom.