Capacity requirements of ring, 1+1, and mesh configurations

SPECIAL REPORTS / Optical Networking/WDM

Carriers are faced with the dilemma of selecting one or a mix of configurations that most effectively and efficiently address their requirements, network topology, and demand profile.

SHAHROKH SAMIEIAN, DR. ZBIGNIEW BOGDANOWICZ, DR. RAMU RAMAMURTHY, DR. SID CHAUDHURI, and DR. KRISHNA BALA, Tellium Inc.

Traditionally, carriers have deployed SONET bidirectional line-switched rings (BLSRs) in their long-haul optical networks. SONET BLSRs have been around for several years; they are well understood, and the literature in this field is abundant. This configuration will continue to be used in the future due to the reliability and fast switching time (50 msec) inherent in the SONET BLSR technology. However, the rate at which SONET BLSRs are deployed will substantially decrease because of its many drawbacks.

First, from the capacity planning perspective, manually selecting rings is a nightmare. Planning tools with complex optimization algorithms have been developed to solve this problem. However, in practice, carriers have often ignored the planning tool results and instead have used their own ad-hoc methods, based on experience, intuition, and common sense, to select rings. Second, from the operations standpoint, carriers often find it simpler to stack new rings to serve incremental demands than to recover the unused and available bandwidth of the existing rings. The result of this approach is a much wasted and unused working capacity of rings.

Many real long-haul-carrier networks are meshed, both physically and logically. A network architecture that is also meshed seems to be a natural choice. Surprisingly, mesh architecture in optical networks is in its infancy, with many standards yet to be defined by standards bodies yet to be created.

A quantitative comparison of the capacity requirement of ring, 1+1, and mesh configurations-with sensitivity analysis of each with respect to fiber connectivity and demand fanout rate (see the sidebar, "Terminology," for definitions of these terms)-illustrates why mesh networking promises to become the architecture of choice in long-haul networks.

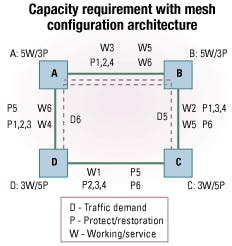
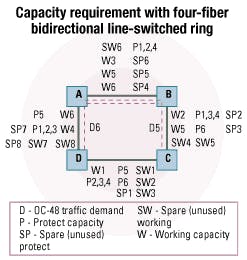
Before examining a larger network, we will compare the various configurations using a small network where we can manually count ports and quickly analyze the differences. Consider a four-node network with the physical loop topology that is logically fully meshed, or in other words, with traffic demands between every pair of nodes. The demand granularity can be anything, but for the sake of argument, we can assume OC-48 traffic. The capacity requirements for 1+1, ring, and mesh architectures are compared.

Figure 1. A network based on 1+1 protection does not allow sharing of protection capacity. In the configuration above, total port count is 48.

In the case of 1+1, protection is dedicated and there is no sharing between protection channels (see Figure 1). The number of required service and restoration ports is 16 and 32, respectively, for a total port requirement of 48. The configuration requires 24 1+1 terminals.

Figure 2. In mesh, the port count shrinks significantly, because protection/restoration capacity can be shared.

With the same network, consider the mesh architecture (see Figure 2). The number of required service and restoration ports is the same, and it is 16, for a total port count of 32. In fact, with a physical loop topology, if can be shown by induction that with mesh configuration, the working and restoration port counts are equal. In this example, we could use four optical switches running mesh restoration, and overall 32 ports are required to serve all six traffic demands.

Figure 3. With a four-fiber bidirectional line-switched ring, 50% of the working bandwidth is wasted.

Next, we examine three different ring designs. First, we consider the widely deployed four-fiber BLSR with OC-192 line rate and OC-48 tributary rate (see Figure 3). Each add/drop multiplexer (ADM) can drop eight OC-48s, four from either side. Four ADMs would serve all six traffic demands. However, we are left with eight unused OC-48 working channels, or exactly 50% wasted working bandwidth. Similarly, the same number of protect capacity is wasted. This simple example shows the inflexibility of the four-fiber OC-192 BLSR and the resulting wasted bandwidth.

Figure 4. A two-fiber bidirectional line-switched ring wastes even more bandwidth than a four-fiber configuration, which may account for its limited deployment.

Much like the four-fiber BLSR, the less widely deployed two-fiber BLSR also suffers from the very same inflexibility (see Figure 4). In this case, each ADM can drop four OC-48s, two from either side. Two stacked rings would be required to serve all six traffic demands. The first ring is left with two unused OC-48 working capacity, or exactly 25% wasted working bandwidth. The second ring is left with six unused OC-48 working channels, or exactly 75% wasted working bandwidth. Also, note the unused OC-48 protection capacity that is again merely required to form the BLSRs.

Since unidirectional path-switched rings are typically not deployed in the long-haul transport network, we did not study them in our modeling.

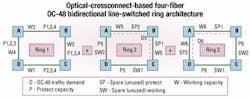
Of course, digital crossconnects or optical crossconnects (OXCs) can be configured to run multiple rings over the same set of switches. If we are to serve the traffic demands using OXC-based four-fiber OC-48 BLSRs, we need three stacked rings. The first ring is full, but the second and third rings each have two unused OC-48 working channels, or exactly 50% wasted working bandwidth. Similarly, the second and third rings also have two unused OC-48 protect channels, or exactly 50% wasted protect bandwidth.

Figure 5. Optical crossconnects may be used in a four-fiber bidirectional line-switched ring. Again, this topology strands significant capacity.

Overall, 24 working and 24 protect ports are required, despite the fact that some of these ports are only required to form the ring-which is exactly why with the ring configuration, more working capacity is required when compared to 1+1 or mesh configurations. And with the ring configuration, exactly half the capacity must be reserved for protection.

Keep in mind that the ring architecture here refers to the OXC-based four-fiber BLSR where the line and tributary rates are both OC-48.

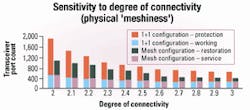
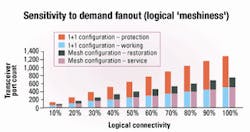
Having studied a simple network and compared the capacity requirements of different configurations, we now examine a larger, hypothetical 20-node network to investigate the sensitivity to degree of connectivity as well as to demand fanout. Links are added or removed to analyze sensitivity to degree of connectivity, or physical "meshiness." Then, traffic demands are added or removed to analyze sensitivity to demand fanout, or logical meshiness.

Figure 6. This chart displaces different topologies in a hypothetical 20-node network with a fanout rate of 50%. The degree of connectivity rises from 2 at left to 3. The mesh configuration can be seen to be more efficient than the 1+1 architecture.

With a fanout rate of 50%, as the degree of connectivity increases from 2 to 3, the required service port consistently decreases in both the 1+1 and ring configurations (see Figure 6). This trend is intuitive, as the service route uses the shortest path in both configurations. As the degree of connectivity increases, shorter paths become available for the service/working routes.

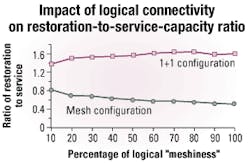
The more significant finding is the rate at which the required restoration ports de creases in the case of mesh architecture. It reduces substantially, because as the network becomes highly connected, more candidate traffic demands are found that can share all or at least a part of their restoration route. With the degree of connectivity of 2.5 or higher, the network requires fewer restoration ports than service ports. In a physically well-connected network, smaller diversely routed 1+1 systems can also be deployed, requiring fewer working and protection ports. However, since there is no capacity sharing, the required protection capacity remains much higher than the working capacity even when the degree of connectivity of the network is high.

Figure 7. The ratio of restoration to service ports in mesh architectures is superior to 1+1 architectures, particularly as the degree of connectivity increases.

Figure 7 shows how the ratio of restoration to service ports compares in the two architectures as a function of degree of connectivity. In the mesh configuration, with a degree of connectivity of 2.5 or higher, this ratio consistently decreases to less than 1. But as expected, in the case of 1+1, this ratio decreases, but it remains well above its theoretical lower bound of 1.

Figure 8. As logical connectivity increases, so does transceiver port count. When the network becomes 80% or more logically meshed, mesh architectures provide a 3:1 savings in required restoration capacity.

Next, we investigate the sensitivity to demand fanout with the degree of connectivity fixed at 3 (see Figure 8). The demand fanout is varied from 10% to a fully connected 100%. We observe that compared to 1+1, the mesh architecture enables a 3:1 savings in restoration capacity requirement when the network is 80% or more logically meshed.

Figure 9. The more logically dense the network becomes, the lower the ratio of restoration ports to service ports in a mesh network.

Figure 9 shows that with the mesh architecture, the ratio of restoration port to service port continually decreases as the network shifts from logically sparse to logically dense, since sharing of the restoration capacity increases. For the mesh configuration, this ratio consistently is less than 1, while for 1+1, it is well above 1.

The configuration we have not compared is the ring architecture. Next, with a large carrier's network, we will include ring in our architecture capacity comparison to complete our analysis.

For this study, we use a generally available network of a large long-haul carrier in the United States, including the cities they serve with their existing fiber topology. We then plan the capacity requirements via each of the three architectures with the assumption that the network is nearly 50% logically meshed. The selected network has 75 cities with 93 fiber links-a modest degree of connectivity of 2.48.

The assumption for the ring topology is that we are running four-fiber OC-48 BLSRs using OXCs. Each ring can drop one OC-48 working channel from either side. We'll assume two core rings with nine regional rings connected to the core rings. Each region is connected to a core ring through two gateway nodes. The traffic demand leaving each region is split into origination-to-hub, hub-to-hub, and hub-to-destination. Next, we need to fill rings and stack them when necessary.

Figure 10. Looking at a real carrier's network, mesh architectures provide overall savings compared to both 1+1 and ring topologies.

Generally, in the traffic distribution least favorable to a ring architecture, one ring would at most serve two traffic demands; in most favorable traffic distribution, one ring would serve as many as the number of nodes in the ring. In a real network, the traffic distribution would be somewhere between the two. However, as mentioned earlier, in practice (for the ease of capacity planning, circuit provisioning, and network management), network operators do not completely fill each ring before stacking the next.

So how many traffic demands should we assume each ring could serve? Generally, we can calculate the average length of a working traffic demand and prove that it is N/4, where N is the number of nodes in the ring. Since the circumference of the ring is N, then four demands on average can be routed in every ring. In our network modeling for rings, we made this assumption. We realize that in the case of all node-to-adjacent-node traffic patterns, the number of demands served by each ring is N. However, our experience shows that carriers typically route fewer demands per ring than we assumed. In other words, it can be argued that we made a non-conservative, ring-favorable fill assumption.

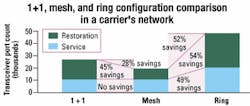
This particular network is not highly connected in the physical sense. More over, we assume demand fanout of only 50%. Despite these two factors, we observe that the working and restoration capacity savings of mesh compared to ring are approximately 49% and 54%, respectively. The overall capacity saving of this network is 52%. We previously explained why the service port requirement of ring is higher than 1+1 and mesh. To repeat, the BLSR protocol requires working and protection capacity at every node on the ring even if there is no traffic at that node.

As expected, the service capacity requirement for both 1+1 and mesh are identical, since in both cases the service route uses the shortest path (see Figure 10). However, the savings obtained from sharing restoration capacity is 45%. The overall configuration saving of 1+1 compared to mesh is 28%.

The level of savings that mesh architecture enables by sharing the restoration capacity is influenced by the characteristics of the network, both physically and logically. We have shown qualitatively that as the physical and logical connectivity of the network increases, the candidates for sharing restoration capacity increase and therefore the savings do, as well.

Studies claiming a certain saving of mesh compared to 1+1 or ring should always qualify their statements by also stating how logically meshed the network is as well as its degree of connectivity. These two attributes influence the savings obtained with mesh configuration compared to other configurations.

Most importantly, we quantitatively compared the savings obtained by mesh configuration in a real network. Com paring mesh to ring, we observed that for a 75-city network with the modest degree of connectivity of 2.48 and logical connectivity of 50%, we obtained 49% service/ working capacity saving, 54% restoration/ protection ca pa city savings, and overall 52% savings. Some European networks have a much higher degree of connectivity-on the order of four or even higher. Such networks lend themselves very well to the mesh architecture.

Shahrokh Samieian is senior network architect at Tellium Inc. (Oceanport, NJ). He can be reached at [email protected]. Also at Tellium, Dr. Zbigniew Bogdanowicz leads the Planning and Simulation Tools Group at Tellium, Dr. Ramu Ramamurthy works on the design of algorithms and protocols for dynamic provisioning and restoration in optical networks, Dr. Sid Chaudhuri leads the network architecture department to develop mesh-networking protocols for restoration and dynamic provisioning and network planning and simulation tools, and Dr. Krishna Bala is a founder, chief technical officer, and lead system architect.

T.E. Stern and K. Bala, Multiwave length Optical Networks: A Layered Approach, Reading, MA, Addison Wesley, 1999.
S. Ramamurthy, Z. Bogdanowicz, S. Samieian, D. Saha, B. Rajagopalan, S. Sengupta, S. Chaudhuri, and K. Bala, "Capacity Performance of Dynamic Provisioning in Optical Networks," Journal of Lightwave Technology, January 2001.

"Degree of connectivity" refers to the average physical (fiber) connectivity at each node. For example, in a loop, the degree of connectivity for each node is exactly two. As more fiber links are added, the degree of connectivity is increased. In general, a network with N nodes and l fiber links has degree of connectivity equal to 2l/N.

"Demand fanout" refers to the logical connectivity or "meshiness" of the network. In a fully meshed network, the number of demand pairs is N(N-1)/2, where again N is the number of nodes.