Networks take their 'Q' from quality evaluations
Q factor measurements increase in importance as optical networks increase data and rates.
MUNIR BHUIYA, Anritsu
As OC-48/STM-16 (2.5-Gbit/sec), Fibre Channel, and Gigabit Ethernet optical networks propagate the landscape, there are greater challenges to ensuring their performance because of the speed at which they transmit data. Technologies such as DWDM and erbium-doped fiber amplifiers have helped solve many of the concerns associated with the transmission of more and more data at such speeds.
Of equal concern is the quality of the data transmission, in light of the increased capacity and distance that data is now traveling. One of the best ways to measure the data-transmission quality of any digital transmission system is to determine the bit-error-rate (BER) characteristics. But with the introduction of high-quality optical transmission circuits centered mainly on long-distance trunk lines and undersea cables, transmission-path-quality requirements have become extremely important.
BER is greatly influenced by the optical signal-to-noise ratio (OSNR) of the system. OSNR is the ratio between the received signal and the additive noise of the optical link. The higher the OSNR, the lower the BER. Typically, optical-network managers need their networks to operate at low error rates, usually on the order of 1x10-12 to 1x10-15.
Testing the OSNR can be difficult because of the many aspects that contribute to noise in an optical transmission system. Although BER testing is an alternative, it is impractical when testing BERs lower than 10-15. An even greater problem with BER testing is that a single test-even at high data rates-can take a very long time. In fact, a BER test takes at least 27 hours to make BER measurements at 10-15 at 10 Gbits/sec. For these reasons, the Q factor measurement has become the new quality evaluation parameter to approximate the BER and determine the OSNR in a system.
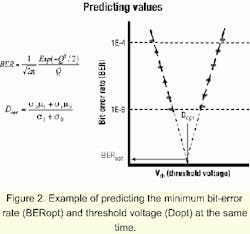
The Q factor theory was announced in 1993 and standardized as ITU-T G.976 Q Factor Measurement Recommendation in 1997. In North America, it was adopted as Recommendation OFSTP-9 TIA/EIA-526-9 in 1999. Today, quality evaluation using the Q factor is increasingly becoming the method of choice for research and development, manufacturing, installation, acceptance inspection, and maintenance of high-quality optical circuits.The Q factor is a measure of the digital signal eye aperture. It adopts the concept of SNR in a digital signal and is an evaluation method that assumes a normal noise distribution (see Figure 1). The Q factor is used to predict the minimum bit-error rate (BERopt) and the threshold voltage (Dopt) at that time (see Figure 2).
Different techniques can be used to conduct Q factor measurements. The oscilloscope method has been used for years and is generally recognized as the fastest and least expensive method. Another benefit of the oscilloscope is the ability to conduct live traffic testing. The major drawback to using an oscilloscope is a failure to always capture every error, which yields misleading results.Using a BER tester in combination with software is another method used to measure Q factor. It can be used to measure the change in the BER as the threshold of the signal is skewed toward either rail. The Q factor can then be calculated from the data. The BER tester method provides more accurate data results than an oscilloscope. But unlike an oscilloscope, a BER tester cannot conduct live traffic testing. A recent complement to the BER tester solution is software that allows users to measure BER as a function of threshold and numerically calculate the optimal value of Q for the system.
The new software makes manually calculated Q measurements a thing of the past, allowing BER analysis to be conducted faster than ever before. Using this software, the noise distribution is measured from the bit-error distribution, and the Q factor is calculated by the method recommended in OFSTP-9/ITU-T G.976. In comparison to measuring the Q factor with a sampling oscilloscope, non-normally distributed noise is eliminated, so an accurate Q factor can be obtained.In addition to making automatic Q factor measurements according to ITU-T G.976 and OFSTP-9, software allows various measured data related to the Q factor to be displayed in relation to BER. For example, Q factor value, BER, optimum BER, and optimum voltage threshold can all be displayed simultaneously. Software also displays µ0, µ1, σ0, σ1, and intermediate data that is obtained at the Q factor calculation and correlated with the normal distribution. When several measurements are performed, statistical data such as maximum, minimum, mean, and distribution can be displayed.
Beyond Q factor measurements, the eye-diagram and eye-margin of the device under test can be measured automatically with new software. As a result, evaluation of optical transmission functions such as eye aperture (ITU-T G.957) by BER measurement becomes very simple, yet is difficult to accurately measure with an oscilloscope.
There are three main elements determining waveform quality: jitter, waveform distortion, and rise/fall speed. The combination of these elements causes waveform degradation, resulting in transmission errors. An eye-diagram measurement is a procedure for evaluating waveforms degraded by these combined factors. This measurement is one typical method for evaluating the quality of digital signals.
In an ideal digital signal, all of these factors should be 0 (zero) and the waveform should be rectangular with perpendicular verticals and horizontals. When there is waveform distortion, the rectangle changes from hexagonal to diamond-shaped to oval, and the section of the open area becomes compressed. That reduces the margin for correct identification of 1s and 0s, which is equivalent to easy generation of errors. Viewed another way, by indicating the area inside the waveform, eye-diagram measurements are a way of guaranteeing a fixed maximum error rate (waveform quality).Traditionally, a digital oscilloscope has been used to measure the eye-diagram. The analog voltage of the input waveform is converted to digital values at the specified sampling cycle and saved to memory (see Figure 3). To reproduce the waveform accurately, sampling must be performed at least twice as fast as the maximum frequency (the Shannon sampling theory). For example, to measure a 10-GHz signal, a sampling frequency of at least 20 GHz is required. Since the input signal includes wideband noise components, however, the required sampling speed exceeds the speed of even today's fastest analog-to-digital converters.
Occasionally, results measured with a digital oscilloscope may not detect errors when performing bit-error measurements, even with a sufficient eye aperture. In this case, the noise observed in the hold time is not "seen" by the oscilloscope. A bit-error detector measures all bits by using a clock signal synchronized with the input signal as a trigger. With an error detector, the bit-error rate is measured at the point specified by clock phase and threshold voltage in the eye-pattern.
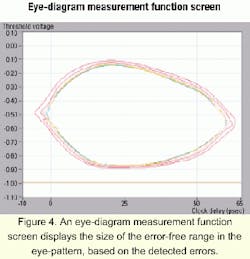
The eye-diagram measurement function (see Figure 4) displays the size of the error-free range in the eye-pattern, based on the detected errors. For eye-diagram-based BER measurements, the clock phase and threshold voltage are varied and the BER at any position in the eye-pattern is measured as a BER contour. Any combination from 10-2x10-15 can be chosen as the contour.This measurement principle achieves a much higher accuracy than the previous method using a sampling oscilloscope. With the eye-diagram measurement function, it is possible to confirm errors up to 10-3 that cannot be confirmed with an oscilloscope. For eye-margin measurements, the margin direction can be set from threshold voltage, clock phase, or both (see Figure 5).
The testing standard is changing accordingly with the market trend toward larger capacity/bandwidth, while focusing on the optimum performance of high-speed optical networks. The industry standard for determining BER characteristics has been Q factor measurements. It offers the best balance of accuracy and efficiency and has traditionally been done using an oscilloscope or BER tester. New advances have been made, however, that have yielded a third method, dubbed auto-correlation, which is also based on BER. As optical networks continue to expand into higher-bandwidth applications such as OC-192 (10 Gbits/sec), the ability to conduct fast BER analysis will become even more imperative. These testing solutions will make such analysis possible, paving the way for optical networks to transmit large amounts of high-quality data.
Munir Bhuiya is a field marketing engineer, digital communications, for Anritsu Co. (Richardson, TX). He can be reached via e-mail at [email protected].